基本介紹
多項式算法是判斷一個算法“好環”的 數學概念。當考察解某一類問題(如線性規劃問題)的一種算法時,在計算機上利用這一 算法解這類問題中的每個具體問題所需的計算次數(時間)是不同的。計算步數(時間)一般與具體問題的規模(如線性規劃問題中變數的個數,約束條件的個數等)有關。為了判 斷一個具體問題規模的大小,往往把此問題 需要輸入計算機的有關數據轉化為一個二進制的代碼序列(即只含0或1組成的序列)。 這個序列中所含0或1的個數L就稱為這一具體問題的輸入長度,並用L來代表此問題的規模大小。
如果解某類問題的一個算法,在解規模為L的具體問題時,其計算步數在最壞的情形下不超過L的一個多項式P(L),則稱這一 算法為 多項式算法(或好算法)。
顯然,在實踐中具有多項式算法的問題才能有效地用計算機計算,因為當問題的規模增大時,所需的計算時間增大的速度還不很大。所以,多項式算法的概念給出了理論上可計算與實際可計算的問題的區別。同時,對某類問題的已知算法,來研究它是否是多項式算法,也具有重要的理論意義和實際意義。
例如,在考察解線性規劃的算法時,克里和明特構造了一個具體的線性規劃問題,說明單純形法不是一個多項式算法。那么,線性規劃問題是否存在多項式算法呢?這一問題首先於1979年由蘇聯的哈奇揚解決。哈奇揚證明了他所提出的橢球算法是一個多項式算法。隨後,在美國工作的印度數學家卡馬卡於1984年又提出了求解線性規劃的另一個多項式算法 。
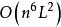 多項式算法
多項式算法1979年,蘇聯數學家哈奇揚在Shor, Levin, Judin等人求解凸規劃方法的思想基礎上,提出了線性規劃中的第一個多項式算法——橢球法, 並且證明:LP可以經多項式次數疊代後找到所求的解,其計算複雜性為。這一成果很快對組合最最佳化、計算理論等領域產生了深遠影響,但在實際計算中該方法卻遠不及單純形法有效, 因為橢球法求解相同規模問題在一般情形下所需要的計算量與在最壞情形下的幾乎差不多,而實際套用中象Klee等人構造的例子幾乎從未遇見過。這就向人們提出了強烈的挑戰:能否找到理論上是“好的”而實際上又是確實可行的算法?
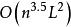 多項式算法
多項式算法於是,在美國貝爾試驗室工作的印度數學家卡馬卡N.Karmarkar (1984) 運用投影變換、勢函式(它是罰函式的變形)等新技巧,創建出一個新的LP多項式算法,其計算複雜性為,大大改進了哈奇揚的結果,很快引起人們的極大關注,人們希望這種方法能比單純形法更有效地解決經濟、管理、工程及其它領域中實際存在的許多大型複雜問題 。
舉例說明
哈奇揚算法
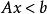 多項式算法
多項式算法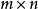 多項式算法
多項式算法哈奇揚方法為考慮如下特徵的問題:求x使之滿足,其中A為矩陣,其方法步驟為:
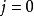 多項式算法
多項式算法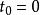 多項式算法
多項式算法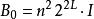 多項式算法
多項式算法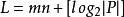 多項式算法
多項式算法1.(初始準備) 記錄疊代次數,t為第j次疊代的解,初始解為分量全為0的n維列向量,取為n階對角矩陣,其中I為n階單位陣,為問題的規模,P為矩陣A及向量b中所有非零分量的乘積,在上述數據中,可逆方陣B是構造橢球的關鍵成分,初始橢球
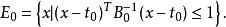 多項式算法
多項式算法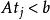 多項式算法
多項式算法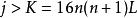 多項式算法
多項式算法2.(檢驗) 若t滿足,則停止疊代,當前解即為所求,若,則停止疊代,說明問題無解。
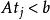 多項式算法
多項式算法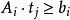 多項式算法
多項式算法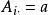 多項式算法
多項式算法3.(疊代) 任選一個不滿足的不等式,例如,並記,設
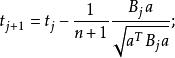 多項式算法
多項式算法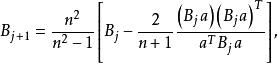 多項式算法
多項式算法轉至第2步。
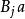 多項式算法
多項式算法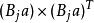 多項式算法
多項式算法為n維列向量,為n×n矩陣,雖然,哈奇揚方法是求解線性規劃的多項式算法,但是其實際疊代上並不產生真實的優越性,這個方法在理論上的影響對線性規劃是突破性的,其後產生了一個新方向,即考慮以約束區域的內點為途徑,去搜尋問題的解,這個方向把線性規劃與非線性規劃以及組合規劃能夠更緊密地結合起來。
卡馬卡算法
1984年,印度數學家N.Karmarkar針對線性規劃問題提出了一種新的多項式時間算法,在實際計算效率方面,Karmarkar算法顯示出可與單純形法競爭的巨大潛力,Karmarkar算法的提出是線性規劃理論研究的突破,而且對於處理非線性最佳化問題也顯示出強大的生命力和廣闊的套用前景。
單純形法是通過檢查可行域邊界上的極點的方法來求解(LP)問題,而Karmarkar算法則是建立在單純形結構之上的,該算法從初始內點出發,沿著最速下降方向,通過可行域內部直接達到最優解,因此,Karmarkar算法也被稱為內點法,由於是在可行域內部尋優,故對於大規模線性規劃問題,當約束條件和變數數目增加時,內點算法的疊代次數變化較少,收斂性和計算速度均優於單純形法。
卡馬卡算法考慮如下標準形式的線性規劃問題
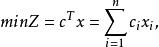 多項式算法
多項式算法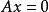 多項式算法
多項式算法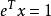 多項式算法
多項式算法滿足及或者
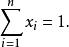 多項式算法
多項式算法這裡e為分量全為1的n維列向量,並且已知:
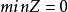 多項式算法
多項式算法1.在上述約束條件下;
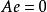 多項式算法
多項式算法2.;
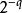 多項式算法
多項式算法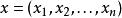 多項式算法
多項式算法3.對於給定精度,當可行解滿足條件
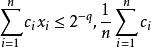 多項式算法
多項式算法時,即可停止疊代,並認為x即為所求的解。

