定義
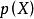多項式分裂域域K上的多項式分裂域 是K的擴展域，其中p因子成為線性因子。
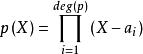多項式分裂域對於每個i我們有
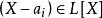多項式分裂域
多項式分裂域 多項式分裂域其中 不一定是不同的，並且使得根 在K上產生L。擴展域L是在K上的最小維度的擴展，其中p分裂。 可以看出，這樣的分裂域存在並且是同構的。 這種同構的自由度被稱為p的伽羅瓦群（如果我們假設它是可分離的）。
事實
作為K上的一組多項式p(X)的分裂域的擴展域L被稱為K的正常擴展。
給定包含K的代數閉合域A，在K和A之間有一個第一無二的p的分裂域L，它們是由p的根生成的。如果K是複數的子域，那么它就是存在的。另一方面，代數閉包的存在通常通過從分裂域結果“傳遞到極限”來證明，因此需要獨立的證據來避免循環推理。
給定K的可分離延伸K'，K'的伽羅瓦閉包L是分裂域的一種類型，並且在顯著意義上也是包含K'的K的伽羅瓦擴展。 這樣的伽羅瓦閉包應該包含K的所有多項式p的分裂域。
構建分裂域
目的
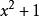多項式分裂域從古希臘時代起，尋找多項式的根一直是一個重要問題。 然而，一些多項式，例如實數域上的 ，實數域上沒有根。 通過構建這樣的多項式的分裂域，可以在新的域中找到多項式的根。
構建
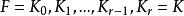多項式分裂域
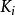多項式分裂域
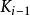多項式分裂域 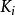多項式分裂域令F為域，p(X)是維度為n的多項式環中的多項式。 構建K的一般過程是構造一個域F的序列 ，使得 是包含p(X)的新根的 的擴展。 由於p(X) 的根最多為n個，所以構建最多需要n個擴展。 構建 的步驟如下：
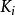多項式分裂域
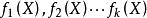多項式分裂域（1）將 上的p(X) 因式分解為不可約因子 。
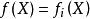多項式分裂域（2）選擇任何非線性不可約因子 。
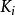多項式分裂域
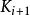多項式分裂域
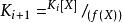多項式分裂域
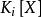多項式分裂域（3）構建 的擴展域 作為商環 ，其中(f(X)) 表示由f(X) 生成的
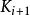多項式分裂域（4）對 重複以上過程直到p(X) 成為完全因子。
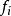多項式分裂域商構建中使用的不可約因子 可以任意選擇。 雖然不同的因素選擇可能導致不同的子域序列，但是所得到的分裂域將是同構的。
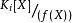多項式分裂域
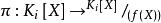多項式分裂域由於f(X) 是不可約的，所以(f(X)) 是最大理想，因此實際上 是一個域。 此外，如果我們令： 是環到其商的自然投影。
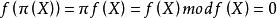多項式分裂域所以π(X)是f(X) 和p(X) 的根。
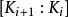多項式分裂域
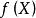多項式分裂域單個擴展域 的維度等於不可約因子 的維度。
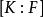多項式分裂域
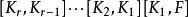多項式分裂域擴展 的維度由 給出並且最多是n！
域
Ki [X]/(f(X))
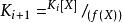多項式分裂域 多項式分裂域如上所述，商環 是當 不可約時的域。 它的元素是形式
多項式分裂域
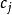多項式分裂域 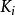多項式分裂域
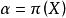多項式分裂域其中 在 里 。
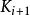多項式分裂域 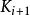多項式分裂域 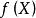多項式分裂域 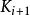多項式分裂域
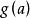多項式分裂域
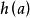多項式分裂域
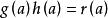多項式分裂域
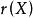多項式分裂域
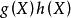多項式分裂域 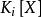多項式分裂域 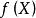多項式分裂域的元素可以被認為是維度小於n的多項式。通過多項式加法的規則給出 中的加法，並且通過多項式乘法 給出乘法。 也就是說，對於在 中的 和 ，產物 其中 是 的剩餘部分由 中的 表示。
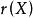多項式分裂域 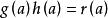多項式分裂域剩餘 可以通過多項式的長分割來計算，但是也可以直接計算 的直接還原規則。 首先讓
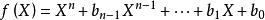多項式分裂域 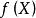多項式分裂域 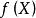多項式分裂域多項式在一個域上，所以可以使 變為摩尼而不失一般性。 現在α是 的根，所以
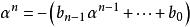多項式分裂域 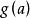多項式分裂域 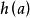多項式分裂域
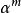多項式分裂域如果產品 具有m≥n的項 ，則可以減少如下：
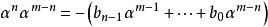多項式分裂域舉例
複數
多項式分裂域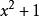 多項式分裂域
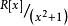多項式分裂域
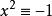多項式分裂域 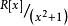多項式分裂域
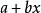多項式分裂域 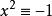多項式分裂域
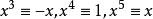多項式分裂域
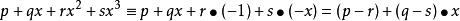多項式分裂域考慮多項式環 和不可約多項式 。商環 由等式 給出。 因此， 的元素（或等價類）是 的形式，其中a和b屬於R。請注意，由於 ，接下來有 等; 因此，例如 。
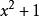多項式分裂域加法和乘法運算首先使用普通多項式加法和乘法，然後減少模 ，即使用
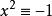多項式分裂域 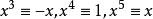多項式分裂域， 等。因此：
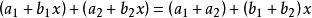多項式分裂域
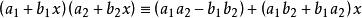多項式分裂域
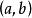多項式分裂域 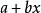多項式分裂域如果我們用 識別 ，那么我們看到加法和乘法由下面給出
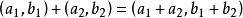多項式分裂域
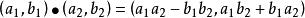多項式分裂域 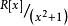多項式分裂域
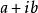多項式分裂域
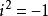多項式分裂域我們聲稱，作為一個域，商 與複數是同構的。一般複數形式為 ，其中a和b是實數， 。 加法和乘法由
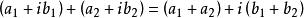多項式分裂域
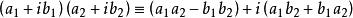多項式分裂域相應的，也可以寫成括弧的形式。
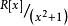多項式分裂域 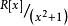多項式分裂域
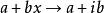多項式分裂域 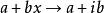多項式分裂域
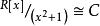多項式分裂域以前的計算表明，加法和乘法在 和C中的方式相同。實際上，我們看到 與C之間的映射 是相加和乘法的同態。意味著 是雙射同態，即同構。 因此，如所要求的： 。
在1847年，柯西使用這種方法來定義複數。
立方的例子
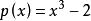多項式分裂域
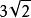多項式分裂域令K為有理數域Q並且 。p的每個根等於 倍立方體的單位根。 因此，如果我們表示統一的立方體根：
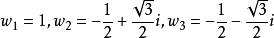多項式分裂域
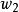多項式分裂域
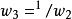多項式分裂域 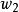多項式分裂域包含p的兩個不同根的任何域將包含兩個不同的立方體根之間的商。 這樣一個商就是一個原始的立方根，即 或 。 因此，p的分裂域L將包含 ，以及2的真實立方根；相反，包含這些元素的Q的任何擴展都包含p的所有根。 從而
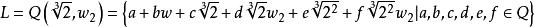多項式分裂域
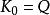多項式分裂域
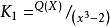多項式分裂域
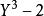多項式分裂域
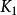多項式分裂域 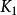多項式分裂域
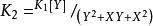多項式分裂域請注意，將上一節中概述的構建過程套用於此示例，從 開始構建該域 。此域不是分裂域，但包含一個（任意）根。然而，多項式 在 上不是不可約的。請注意，X不是不確定的，實際上是 的元素。現在，繼續這個過程，我們得到 這確實是分裂域。
