定義
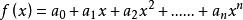 本原多項式
本原多項式 本原多項式
本原多項式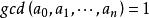 本原多項式
本原多項式 本原多項式
本原多項式 本原多項式
本原多項式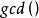 本原多項式
本原多項式設是唯一分解整環 上的多項式,如果 ,則稱 為 上的一個本原多項式 。(符號表示最大公約數)
本原多項式滿足以下條件:
 本原多項式
本原多項式1)是既約的,即不能再分解因式;
 本原多項式
本原多項式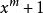 本原多項式
本原多項式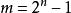 本原多項式
本原多項式2)可整除,這裡的;
 本原多項式
本原多項式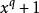 本原多項式
本原多項式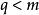 本原多項式
本原多項式3)不能整除,這裡。
定理
高斯引理:本原多項式的乘積還是本原多項式。
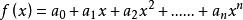 本原多項式
本原多項式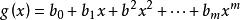 本原多項式
本原多項式證明:設 和 分別是n次與m次的本原多項式。
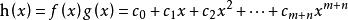 本原多項式
本原多項式令
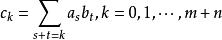 本原多項式
本原多項式其中
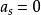 本原多項式
本原多項式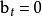 本原多項式
本原多項式這裡,當s>n或t>m時,規定 及 。
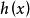 本原多項式
本原多項式 本原多項式
本原多項式 本原多項式
本原多項式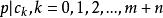 本原多項式
本原多項式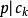 本原多項式
本原多項式 本原多項式
本原多項式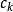 本原多項式
本原多項式假定 不是本原的,則存在 上的不可約元 ,使。(式表示整除)
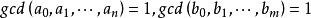 本原多項式
本原多項式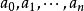 本原多項式
本原多項式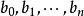 本原多項式
本原多項式 本原多項式
本原多項式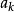 本原多項式
本原多項式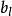 本原多項式
本原多項式已知 ,設 及 中最先一個不能被整除的元素分別為 與 ,則
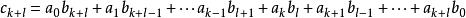 本原多項式
本原多項式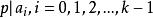 本原多項式
本原多項式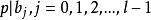 本原多項式
本原多項式 本原多項式
本原多項式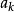 本原多項式
本原多項式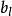 本原多項式
本原多項式 本原多項式
本原多項式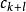 本原多項式
本原多項式 本原多項式
本原多項式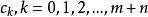 本原多項式
本原多項式因為且,而 不整除 、 ,所以 不整除 ,這與能整除矛盾。
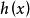 本原多項式
本原多項式這就證明了 為本原多項式。
套用
1)在MATLAB中,本原多項式可以通過函式primpoly(x)來產生。
2)在MATLAB中,通過函式gfprimfd(m,'min')可以找到一個最小的本原多項式。

