高次代數方程求根

左邊為多項式的方程，稱為n次代數方程，又稱多項式方程,其中n=1,2,…；αk是實係數或復係數,α0≠0。當n>1時,它叫做高次代數方程,其次數就是n。多項式的零點就是對應代數方程的根。代數基本定理說，復係數代數方程在複數域至少有一個根。如果x1是一個根,則Pn(x)一定可被(x-x1)所除盡，其商為(n-1)次多項式。如果n>1，其商至少又有一個根x2,它也是原來方程的一個根。因此n次代數方程總是有n個根x1,x2,…,xn,其中可能有相同的根,叫做重根。

高次代數方程求根

正文

二次方程可以用公式求根，公式內包含某數的平方根；標準三次方程也可以用公式求根，公式內包含三次根；標準四次方程的對應多項式可以分解成兩個二次式的乘積，其係數在求出對應三次方程的一個根後也可用公式求出；五次及五次以上的代數方程一般不能用根式求解。
將超越方程ƒ(x)=0左端換成多項式Pn(x),超越方程就變成高次代數方程。因此超越方程求根的各種方法，例如割線法、牛頓法均可用於求高次代數方程的根（見超越方程數值解法）。下面是利用多項式性質的三種求根方法。
劈因子法　用x的二次式

除Pn(x)則得商Q(x)及餘式

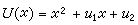
r(x)=r1(x)+r2，

因而有

Pn(x)=U(x)Q(x)+r(x)。 (1)

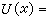
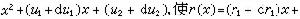
設U(x)是一個近似二次因式，問題是怎樣修改u1和u2使對應的餘式更接近於零。為此，作線性近似，取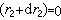則修正量du1、du2應滿足方程組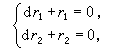

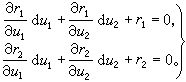進一步可寫為

　 (2)

利用已知關係可求出代入(2)後，就能求出u1和u2的校正量du1和du2。而u1+du1、u2+du2就是更好的二次因式的兩個係數。
伯努利法　設E是使數列Fk的下標增加1的運運算元,即

EFk=Fk+1，

則齊次常係數線性差分方程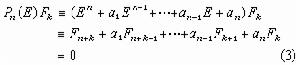

的特徵方程就是代數方程Pn(x)=0，這個代數方程的根x1,x2,…,xn叫做差分方程的特徵根。
給定 (F0,F1,…,Fn-1)的定值例如(0, 0,…,1)即可依次從(3)算出Fn,Fn+1,…。這樣就定出差分方程的一個特解。
如果特徵根各不相同，則差分方程的一般解是

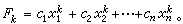
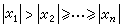設，且с1≠0，則當k→∞時,特解Fk的主要項是第一項，即

,

這就是求最大實根x1的伯努利法。
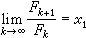設方程的最大根是一對共軛復根： 　

計算

可以證明：

，

由此可得最大共軛復根對應的近似二次因式：

。

勞思表格法　設給定代數方程 Pn(x)=0的係數都是實數，其中α0=1。勞思表格的計算方法如下：

其他行的數的計算公式為

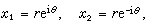
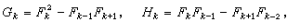
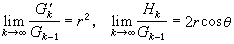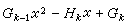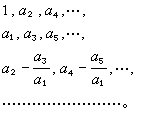
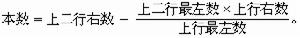
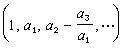利用勞思表格可以對根的位置作出判斷。如果勞思表格上最左列自上而下 n+1個數均為正數，則虛軸上及右半複平面上都沒有根；否則虛軸上或右半複平面上有根。設最左列係數都不等於零，則可以證明在虛軸上沒有根，在右半平面上根的個數等於在左列係數的變號次數。利用勞思表格還可以求出最大實部根的實部。設用 Pn(x)的係數作出的勞思表格不滿足最左列係數都為正的條件，則知在右半閉複平面上有根。把複平面的原點平移到新原點(α,0),求出Pn(x)在α點的展開式係數，利用新係數構造在α點的勞思表格。選α充分大，則在新原點的右半平面沒有根，最大實部根的實部必在區間(0,α)內。構造在α/2點的勞思表格，如果在右半平面有根，則最大實部根的實部在區間 (α/2,α)內，否則在區間(0, α/2)內。在有最大實部根的區間用中點繼續分割及判斷，則可得到最大實部根的實部的充分好的近似值。如果最大實部根是一個實根，所得值就是這個實根的近似值，否則它是有最大實部的一對或幾對共軛復根的實部的近似值，而共軛復根的虛部可以從最後點的勞思表格內求出。
設Pn(x)的勞思表格判明在右半平面上沒有根,則在負實軸上選新原點-α 。選α充分大, 則在新原點的右半平面上有根，最大實部根的實部在(-α,0)區間內。用中點分割法可以求出最大實部根。
在高次代數方程求根的過程中，往往會遇到病態多項式，它的係數的微小變化會引起零點的很大變化。因此，在電子計算機上編制通用求根程式時，計算機運算必須按高精度進行，即至少用雙倍精度進行。
若已求出多項式 Pn(x)的一個實零點或一對共軛復零點，就可以用綜合除法將原多項式化成一低次的多項式，這樣可以依次求出Pn(x)的n個零點。但是，降階運算帶來了誤差積累。如果求根次序按模從大到小進行，則降階過程中引入的誤差對後面一些小根精度的影響可能是嚴重的；但如果按從小到大的次序進行，即使對於病態多項式，一般也不會影響後面求的根的精度。
參考書目
　清華大學、北京大學《計算方法》編寫組編：《計算方法》，上冊，科學出版社，北京，1974。

配圖

相關連線