通俗方法
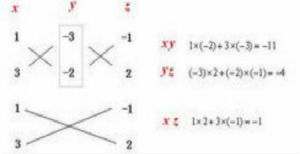 十字相乘法
十字相乘法例:
a²x²+ax-42
首先,我們看看第一個數,是a²,代表是兩個a相乘得到的,則推斷出(a×+?)×(a×+?),
然後我們再看第二項,+a這種式子是經過合併同類項以後得到的結果,所以推斷出是兩項式×兩項式。
再看最後一項是-42,-42是-6×7或者6×-7也可以分解成-21×2或者21×-2。
首先,21和2無論正負,通過任意加減後都不可能是1,只可能是-19或者19,所以排除後者。
然後,再確定是-7×6還是7×-6。
(a×-7)×(a×+6)=a²x²-ax-42(計算過程省略)
得到結果與原來結果不相符,原式+a變成了-a。
再算:
(a×+7)×(a×+(-6))=a²x²+ax-42
正確,所以a²x²+ax-42就被分解成為(ax+7)×(ax-6),這就是通俗的十字相乘法分解因式。
例題解析
例1
把2x²-7x+3分解因式。
分析:先分解二次項係數,分別寫在十字交叉線的左上角和左下角,再分解常數項,分
別寫在十字交叉線的右上角和右下角,然後交叉相乘,求代數和,使其等於一次項係數。
分解二次項係數(只取正因數因為取負因數的結果與正因數結果相同!)。
2=1×2=2×1;
分解常數項:
3=1×3=3×1=(-3)×(-1)=(-1)×(-3).
用畫十字交叉線方法表示下列四種情況:
13
╳
21
1×1+2×3=7≠-7
11
╳
23
1×3+2×1=5≠-7
1-1
╳
2-3
1×(-3)+2×(-1)=-5≠-7
1-3
╳
2-1
1×(-1)+2×(-3)=-7
經過觀察,第四種情況是正確的,這是因為交叉相乘後,兩項代數和恰等於一次項係數-7。
解2x²-7x+3=(x-3)(2x-1)
通常地,對於二次三項式ax²+bx+c(a≠0),如果二次項係數a可以分解成兩個因數之積,即a=a1a2,常數項c可以分解成兩個因數之積,即c=c1c2,把a1,a2,c1,c2,排列如下:
a1c1
╳
a2c2
a1c2+a2c1
按斜線交叉相乘,再相加,得到a1c2+a2c1,若它正好等於二次三項式ax²+bx+c的一次項係數b,即a1c2+a2c1=b,那么二次三項式就可以分解為兩個因式a1x+c1與a2x+c2之積,即
ax^2+bx+c=(a1x+c1)(a2x+c2)
像這種藉助畫十字交叉線分解係數,從而幫助我們把二次三項式分解因式的方法,通常叫做十字相乘法.
例2
把5x²+6xy-8y²分解因式.
分析:這個多項式可以看作是關於x的二次三項式,把-8y²看作常數項,在分解二次項及常數項係數時,只需分解5與-8,用十字交叉線分解後,經過觀察,選取合適的一組,即
12
╳
5-4
1×(-4)+5×2=6
解5x²+6xy-8y²=(x+2y)(5x-4y).
指出:原式分解為兩個關於x,y的一次式。
例3
把(x-y)(2x-2y-3)-2分解因式.
分析:這個多項式是兩個因式之積與另一個因數之差的形式十字相乘法,只有先進行多項式的乘法運算,把變形後的多項式再因式分解。
問:以上乘積的因式是什麼特點,用什麼方法進行多項式的乘法運算最簡便?
答:第二個因式中的前兩項如果提出公因式2,就變為2(x-y),它是第一個因式的二倍,然後把(x-y)看作一個整體進行乘法運算,可把原多項式變形為關於(x-y)的二次三項式,就可以用十字相乘法分解因式了。
解(x-y)(2x-2y-3)-2
=(x-y)[2(x-y)-3]-2
=2(x-y)²-3(x-y)-2
1-2
╳
21
1×1+2×(-2)=-3
=[(x-y)-2][2(x-y)+1]
=(x-y-2)(2x-2y+1).
指出:將元x、y換成(x+y),以(x+y)為元,這就是“換元法”。
教學重點
重點:正確地運用十字相乘法把某些二次項係數不是1的二次三項式分解因式。
教學難點
難點:靈活運用十字相乘法分解因式。
原理
一個集合中的個體,只有2個不同的取值,部分個體取值為A,剩餘部分取值為B。平均值為C。求取值為A的個體與取值為B的個體的比例。假設總量為S,A所占的數量為M,B為S-M。
則:[A*M+B*(S-M)]/S=C
A*M/S+B*(S-M)/S=C
M/S=(C-B)/(A-B)
1-M/S=(A-C)/(A-B)
因此:M/S∶(1-M/S)=(C-B)∶(A-C)
上面的計算過程可以抽象為:
A^C-B
^C
B^A-C
這就是所謂的十字相乘法。X增加,平均數C向A偏,A-C(每個A給B的值)變小,C-B(每個B獲得的值)變大,兩者如上相除=每個B得到幾個A給的值。即比例,以十字相乘法形式展現更加清晰。
注意事項
第一點:用來解決兩者之間的比例問題。
第二點:得出的比例關係是基數的比例關係。
第三點:總均值放中央,對角線上,大數減小數,結果放在對角線上。
判定
對於形如ax²+bx+c的多項式,在判定它能否使用十字相乘法分解因式時,可以使用Δ=b²-4ac進行判定。當Δ為完全平方數時,可以在整數範圍該對多項式進行十字相乘。
具體套用
雙十字相乘法是一種因式分解方法。對於型如Ax²;+Bxy+Cy²;+Dx+Ey+F的多項式的因式分解,常採用的方法是待定係數法。這種方法運算過程較繁。對於這問題,若採用“雙十字相乘法”(主元法),就能很容易將此類型的多項式分解因式。
例:3x²;+5xy-2y²;+x+9y-4=(x+2y-1)(3x-y+4)
因為3=1×3,-2=2×(-1),-4=(-1)×4,
而1×(-1)+3×2=5,2×4+(-1)(-1)=9,1×4+3×(-1)=1
要訣:把缺少的一項當作係數為0,0乘任何數得0,
例:ab+b²+a-b-2
=0×1×a²+ab+b²+a-b-2
=(0×a+b+1)(a+b-2)
=(b+1)(a+b-2)
提示:設x²=y,用拆項法把cx²拆成mx²與ny之和。
例:2x^4+13x^3+20x²+11x+2
=2y²+13xy+15x²+5y+11x+2
=(2y+3x+1)(y+5x+2)
=(2x²+3x+1)(x²+5x+2)
=(x+1)(2x+1)(x²+5x+2)
分解二次三項式時,我們常用十字相乘法.對於某些二元二次六項式(ax²+bxy+cy²+dx+ey+f),我們也可以用十字相乘法分解因式。
例如,分解因式2x²-7xy-22y²-5x+35y-3.我們將上式按x降冪排列,並把y當作常數,於是上式可變形為
2x²-(5+7y)x-(22y²-35y+3),
可以看作是關於x的二次三項式.
對於常數項而言,它是關於y的二次三項式,也可以用十字相乘法,分解為
即
-22y²+35y-3=(2y-3)(-11y+1).
再利用十字相乘法對關於x的二次三項式分解
所以
原式=〔x+(2y-3)〕〔2x+(-11y+1)〕
=(x+2y-3)(2x-11y+1).
(x+2y)(2x-11y)=2x2-7xy-22y2;
(x-3)(2x+1)=2x2-5x-3;
(2y-3)(-11y+1)=-22y²+35y-3.
這就是所謂的雙十字相乘法.也是俗稱的“主元法”
用雙十字相乘法對多項式ax²+bxy+cy²+dx+ey+f進行因式分解的步驟是:
⑴用十字相乘法分解ax²+bxy+cy²,得到一個十字相乘圖(有兩列);
⑵把常數項f分解成兩個因式填在第三列上,要求第二、第三列構成的十字交叉之積的和等於原式中的ey,第一列、第三列構成的十字交叉之積的和等於原式中的dx.
我們把形如anx^n+a(n-1)x^(n-1)+…+a1x+a0(n為非負整數)的代數式稱為關於x的一元多項式,並用f(x),g(x),…等記號表示,如
f(x)=x²-3x+2,g(x)=x^5+x²+6,…,
當x=a時,多項式f(x)的值用f(a)表示.如對上面的多項式f(x)
f⑴=12-3×1+2=0;
f(-2)=(-2)²-3×(-2)+2=12.
若f(a)=0,則稱a為多項式f(x)的一個根.
定理1(因式定理)若a是一元多項式f(x)的根,即f(a)=0成立,則多項式f(x)至少有一個因式x-a.
根據因式定理,找出一元多項式f(x)的一次因式的關鍵是求多項式f(x)的根.對於任意多項式f(x),要求出它的根是沒有一般方法的,然而當多項式f(x)的係數都是整數時,即整係數多項式時,經常用下面的定理來判定它是否有有理根。
怎樣進行分解因式
例7x+(-8x)=-x
解:原式=(x+7)(x-8)
例2
-2x+(-8x)=-10x
解:原式=(x-2)(x-8)
例3、
分析:該題雖然二次項係數不為1,但也可以用十字相乘法進行因式分解。
因為
9y+10y=19y
解:原式=(2y+3)(3y+5)
例4、因式分解。
分析:因為
21x+(-18x)=3x
解:原式=(2x+3)(7x-9)
例5、因式分解。
分析:該題可以將(x+2)看作一個整體來進行因式分解。
因為
-25(x+2)+[-4(x+2)]=-29(x+2)
解:原式=[2(x+2)-5][5(x+2)-2]
=(2x-1)(5x+8)
例6、因式分解。
分析:該題可以先將()看作一個整體進行十字相乘法分解,接著再套用一次十字相乘。
因為
-2+[-12]=-14a+(-2a)=-a3a+(-4a)=-a
解:原式=[-2][-12]
=(a+1)(a-2)(a+3)(a-4)

