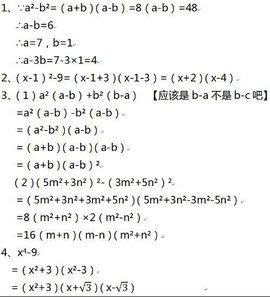方法分類
 因式分解法
因式分解法把一個多項式化為幾個整式的積的形式,這種變形叫做把這個多項式因式分解,也叫作分解因式。因式分解沒有普遍的方法,國中數學教材中主要介紹了提公因式法、公式法。
而在競賽上,又有拆項和添減項法,分組分解法和十字相乘法,待定係數法,雙十字相乘法,對稱多項式輪換對稱多項式法,餘數定理法,求根公式法,換元法,長除法,除法等。
提公因式法
各項都含有的公共的因式叫做這個多項式各項的公因式。 如果一個多項式的各項有公因式,可以把這個公因式提出來,從而將多項式化成兩個因式乘積的形式,這種分解因式的方法叫做提公因式法。 具體方法:當各項係數都是整數時,公因式的係數應取各項係數的最大公約數;字母取各項的相同的字母,而且各字母的指數取次數最低的;取相同的多項式,多項式的次數取最低的。 如果多項式的第一項是負的,一般要提出“-”號,使括弧內的第一項的係數成為正數。提出“-”號時,多項式的各項都要變號。 口訣:找準公因式,一次要提淨;全家都搬走,留1把家守。
要變號,變形看奇偶。
例如:
-am+bm+cm=-m(a-b-c);
a(x-y)+b(y-x)=a(x-y)-b(x-y)=(x-y)(a-b)。
注意:把2a²+1/2變成2(a²+1/4)不叫提公因式
公式法
如果把乘法公式反過來,就可以把某些多項式分解因式,這種方法叫公式法。
平方差公式:a²-b²=(a+b)(a-b);
完全平方公式:a²±2ab+b²=(a±b)²;
注意:能運用完全平方公式分解因式的多項式必須是三項式,其中有兩項能寫成兩個數(或式)的平方和的形式,另一項是這兩個數(或式)的積的2倍。
立方和公式:a³+b³=(a+b)(a²-ab+b²);
立方差公式:a³-b³=(a-b)(a²+ab+b²);
完全立方公式:a³±3a²b+3ab²±b³=(a±b)³.
其他公式:(1)a³+b³+c³+3abc=(a+b+c)(a²+b²+c²-ab-bc-ca)
例如:a² +4ab+4b² =(a+2b)²。
待定係數法
例如,將ax^2;+bx+c(a,b,c是常數,ab≠0)因式分解,可令ax^2;+bx+c=0,再解這個方程。如果方程無解,則原式無法因式分解;如果方程有兩個相同的實數根(設為m),則原式可以分解為(x-m)^2;;如果方程有兩個不相等的實數根(分別設為m,n),則原式可以分解為(x-m)(x-n)。
更高次數的多項式亦可。
例:分解因式x^2;+3x-4。
答:設x^2;+3x-4=0
解方程得:x1=1x2=-4
∴x^2;+3x-4因式分解為(x-1)(x+4)
十字相乘法
十字分解法的方法簡單來講就是:十字左邊相乘等於二次項係數,右邊相乘等於常數項,交叉相乘再相加等於一次項係數。其實就是運用乘法公式(x+a)(x+b)=x²+(a+b)x+ab的逆運算來進行因式分解。
十字分解法能把某些二次三項式分解因式。對於形如ax²+bx+c=(a₁x+c₁)(a₂x+c₂)的整式來說,方法的關鍵是把二次項係數a分解成兩個因數a₁,a₂的積a₁·a₂,把常數項c分解成兩個因數c₁,c₂的積c₁·c₂,並使a₁c₂+a₂c₁正好等於一次項的係數b,那么可以直接寫成結果:ax²+bx+c=(a₁x+c₁)(a₂x+c₂)。在運用這種方法分解因式時,要注意觀察,嘗試,並體會,它的實質是二項式乘法的逆過程。當首項係數不是1時,往往需要多次試驗,務必注意各項係數的符號。基本式子:x²+(p+q)x+pq=(x+p)(x+q)。
技巧
 提公因式法
提公因式法1.分解因式與整式乘法是互為逆變形。
2.分解因式技巧掌握:
①等式左邊必須是多項式;
②分解因式的結果必須是以乘積的形式表示;
③每個因式必須是整式,且每個因式的次數都必須低於原來多項式的次數;
④分解因式必須分解到每個多項式因式都不能再分解為止。
註:分解因式前先要找到公因式,在確定公因式前,應從係數和因式兩個方面考慮。
3.提公因式法基本步驟:
(1)找出公因式;
(2)提公因式並確定另一個因式:
①第一步找公因式可按照確定公因式的方法先確定係數再確定字母;
②第二步提公因式並確定另一個因式,注意要確定另一個因式。
③提完公因式後,另一因式的項數與原多項式的項數相同。