相關概念
單調性
對任一數列{x}，如果從某一項x開始，滿足
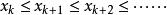單調有界定理則稱數列（從第k項開始）是單調遞增的。特別地，如果上式全部取小於號，則稱數列是 嚴格單調遞增的。
同樣地，如果從某一項k開始，滿足
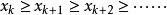單調有界定理則稱數列（從第k項開始）是單調遞減的。特別地，如果上式全部取大於號，則稱數列是 嚴格單調遞減的。
單調遞增數列和單調遞減數列統稱單調數列。
有界性
對任一數列{x}，如果存在某個實數A使不等式
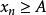單調有界定理恆成立，則稱實數A是數列的一個下界；同樣地，如果存在某個實數B使不等式
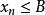單調有界定理恆成立，則稱實數B是數列的一個上界。
如果一個數列既有上界又有下界，則稱這個數列是有界的。此時，存在一個正數M，使不等式
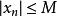單調有界定理成立。
根據數列有界的定義可知，如果一個數列有界，那么它一定有上界和下界。反過來，如果一個數列只有上界或只有下界，則不能得出數列有界的結論。
定理
單調有界數列必有極限。
這個性質是實數連續性的一個體現，可以用實數連續性公理對其進行證明。
證明
設數列{x}單調遞增且有上界，接下來用戴德金定理證明{x}必有極限。
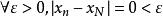單調有界定理分類討論，如果{x}從第N項開始所有的項都相等（即數列有無窮多個相等的項），那么由於數列是單調遞增的，當n>N時，有x=x，因此對 。即{x}收斂到x。
如果{x}中只有有限項相等，即數列從某項開始嚴格單調遞增，那么因為{x}有上界，可取所有{x}的上界組成一個數集B，並取A=R/B。則：
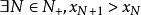單調有界定理
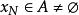單調有界定理①由取法可知數集B非空，而{x}為嚴格單調遞增數列，故 。∴ 。
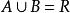單調有界定理② 。
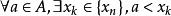單調有界定理③∵A中任何元素都不是{x}的上界，∴ 。
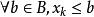單調有界定理又∵B中任何元素都是{x}的上界，∴ 。
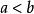單調有界定理故必有 。
∴由戴德金定理可知，存在唯一實數η，使得η要么是A中的最大值，要么是B中的最小值。
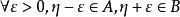單調有界定理但無論是哪種情況， 。
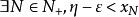單調有界定理
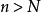單調有界定理
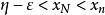單調有界定理④由數集A的意義可知， 。而數列單調遞增，故當 時， 。
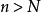單調有界定理
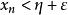單調有界定理⑤由數集B的意義可知，當 時， 。
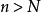單調有界定理綜合④⑤可知，當 時，
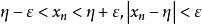單調有界定理
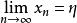單調有界定理∴ ，即{x}有極限。
同理可證：若數列{x}單調遞減且有下界，則{x}必有極限。
套用
在一般的教科書中，單調有界定理是通過確界原理來證明的，即通過確界原理知道{x}有上（下）確界α，再證明{x}收斂於α。事實上，單調有界定理與確界原理等價，既可以由確界原理得到單調有界定理，也可以由單調有界定理得到確界原理。以下是其證法。
問題：試通過單調有界定理證明確界原理。
解：不妨設數集S非空有上界，將所有不小於S中的任一元素的有理數排成一個數列{r}，並令{x}=min{r,r,r...r}。為更直觀理解{x}，舉例如下：
設S=[1,2]。第一次，取r=3，則x=min{3}=3。第二次，取r=5，則x=min{3,5}=3。第三次，取r=2.5，則x=min{3,5,2.5}=2.5。第四次，取r=2.2，則x=min{3,5,2.5,2.2}=2.2……以此類推。顯然{x}單調遞減並且有下界（S中任何元素都是{x}的下界），因此{x}收斂。設極限為η，並且由上述構造可知，η≤x≤r。
利用反證法，
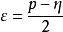單調有界定理
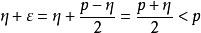單調有界定理①若η不是S的上界，即存在p∈S，使p>η。取 ，根據極限的幾何意義，存在正整數N，使不等式η<x<η+ε成立。而 ，從而x<p。這與x不小於S中的任一元素矛盾。
②任取a>0，若對任意k∈S，都有k≤η-a，根據有理數的稠密性（即任何兩個不相等的實數之間必定存在有理數），存在有理數r，使不等式k≤η-a<r<η成立。因為我們把所有不小於S中的任一元素的有理數排成了一個數列{r}，r∈{r}。這樣一來，就得到η≤r，矛盾。
所以，η是S的上確界。
補充：有理數的稠密性
有理數在實數中是稠密的，即任何兩個不相等的實數之間總存在有理數。（實際上任何兩個不相等的實數之間不僅存在有理數，而且還存在無理數。在這裡暫時不對無理數作討論。）
用數學語言描述為：
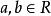單調有界定理 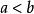單調有界定理
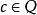單調有界定理
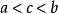單調有界定理若 且 ，則存在 ，滿足 。
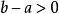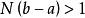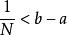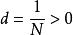單調有界定理
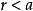單調有界定理
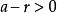單調有界定理
單調有界定理
單調有界定理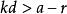
單調有界定理
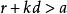單調有界定理
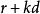單調有界定理
單調有界定理
單調有界定理
單調有界定理 單調有界定理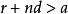
單調有界定理
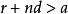單調有界定理 單調有界定理
單調有界定理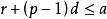
單調有界定理
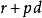單調有界定理證明：因 ，由實數的阿基米德公理，存在正整數 ，使 ，或 。令 ，它是一個有理數。再任取有理數 ，則 。由阿基米德公理，存在自然數 ，使 ，即 。顯然 是有理數，並且對所有大於 的自然數 ，都有 。取使不等式 成立的最小的自然數 （最小指的是 ），則 為所求有理數。
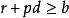單調有界定理
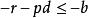單調有界定理 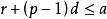單調有界定理如果不是這樣，即假設，那么。將該不等式的兩邊與的兩邊相加，得
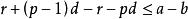單調有界定理去括弧，整理即得
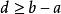單調有界定理
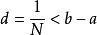單調有界定理這與上面矛盾。
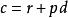單調有界定理 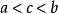單調有界定理這樣就證明了存在有理數，使。
注意事項
（1）單調有界定理只能用於證明數列極限的存在性，如何求極限需用其他方法；
（2）數列從某一項開始單調有界的話，結論依然成立，這是因為增加或去掉數列有限項不改變數列的極限。
