基本介紹
定理
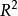 龐加萊一本迪克松定理
龐加萊一本迪克松定理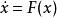 龐加萊一本迪克松定理
龐加萊一本迪克松定理(龐加萊-本迪克松定理) 考慮上的微分方程。
 龐加萊一本迪克松定理
龐加萊一本迪克松定理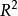 龐加萊一本迪克松定理
龐加萊一本迪克松定理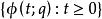 龐加萊一本迪克松定理
龐加萊一本迪克松定理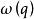 龐加萊一本迪克松定理
龐加萊一本迪克松定理(a)假設在上有定義,正半軌有界,則:(i)含有不動點或(ii)是周期軌。
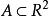 龐加萊一本迪克松定理
龐加萊一本迪克松定理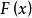 龐加萊一本迪克松定理
龐加萊一本迪克松定理 龐加萊一本迪克松定理
龐加萊一本迪克松定理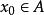 龐加萊一本迪克松定理
龐加萊一本迪克松定理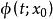 龐加萊一本迪克松定理
龐加萊一本迪克松定理 龐加萊一本迪克松定理
龐加萊一本迪克松定理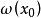 龐加萊一本迪克松定理
龐加萊一本迪克松定理(b)假設是有界閉子集且是微分方程的正不變集,假設在內有定義,但沒有不動點,則對任意的,軌線:(i)是周期軌或(ii)趨於一個周期軌( 當時)且就是該周期軌。
注意點
注1要使平面上的連通區域A既是正不變集又不含有不動點,則它必是含有一個“洞”的環域,這樣它就有兩條邊界,每一邊界都是閉曲線(不必是圓)。
注2為使環域A成為正不變集,只需系統的向量場在邊界上指向環域內部。
注3對上述定理可做適當的變動,即環域A是負不變集,邊界上的軌線都進入A的外部 。
證明思路
這裡敘述證明的關鍵思路,證明需要利用流關於初始值的連續性。
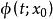 龐加萊一本迪克松定理
龐加萊一本迪克松定理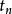 龐加萊一本迪克松定理
龐加萊一本迪克松定理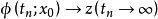 龐加萊一本迪克松定理
龐加萊一本迪克松定理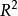 龐加萊一本迪克松定理
龐加萊一本迪克松定理 龐加萊一本迪克松定理
龐加萊一本迪克松定理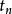 龐加萊一本迪克松定理
龐加萊一本迪克松定理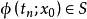 龐加萊一本迪克松定理
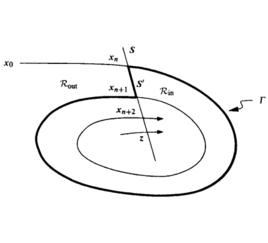
龐加萊一本迪克松定理軌線正向位於A內,勢必不斷地接近於某點z,即存在時間序列使得。這種思想就是數學中的緊性,類似於有界遞增點列一定收斂,於是中的有界點列必須趨近於某點。點z不是不動點,其附近的軌線大致有相同的走向。設為過點z的截線,使得附近其他軌線同向穿過S,則對於充分大的n,總可以調節使得。取一段軌線
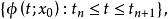 龐加萊一本迪克松定理
龐加萊一本迪克松定理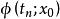 龐加萊一本迪克松定理
龐加萊一本迪克松定理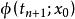 龐加萊一本迪克松定理
龐加萊一本迪克松定理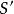 龐加萊一本迪克松定理
龐加萊一本迪克松定理 龐加萊一本迪克松定理
龐加萊一本迪克松定理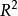 龐加萊一本迪克松定理
龐加萊一本迪克松定理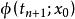 龐加萊一本迪克松定理
龐加萊一本迪克松定理 龐加萊一本迪克松定理
龐加萊一本迪克松定理 龐加萊一本迪克松定理
龐加萊一本迪克松定理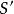 龐加萊一本迪克松定理
龐加萊一本迪克松定理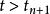 龐加萊一本迪克松定理
龐加萊一本迪克松定理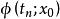 龐加萊一本迪克松定理
龐加萊一本迪克松定理以及S上與之間的線段,它們構成一條閉曲線,該閉曲線將分成兩部分(參見圖1)。從出發的軌線要么進入的外部,要么進入的內部;而從上任一點出發的軌線具有相同的性態。因此當時不可能重新進入其他區域,這意味著軌線與S的交點呈現單調性,它們必從一側收斂於z。進一步分析表明,如果z不是周期的,則附近的軌線不可能返回,故z必須是周期的。
 龐加萊一本迪克松定理
龐加萊一本迪克松定理 龐加萊一本迪克松定理
龐加萊一本迪克松定理由上述證明可在收斂於周期軌方面獲得更多的認識,實際上,若一條軌線在極限環的一側聚集,則龐加萊映射在該側是單調且吸引的。這說明極限環該側附近的軌線的極限集就是該極限環,極限環在該側是軌道漸近穩定的。如果周期軌兩側的軌線的極限集都是該周期軌,則該周期軌就是(兩側)軌道漸近穩定的,即有下述推論 。
 圖1
圖1推論
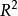 龐加萊一本迪克松定理
龐加萊一本迪克松定理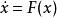 龐加萊一本迪克松定理
龐加萊一本迪克松定理 龐加萊一本迪克松定理
龐加萊一本迪克松定理推論 考慮上的微分方程,假設為孤立的周期軌。
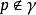 龐加萊一本迪克松定理
龐加萊一本迪克松定理 龐加萊一本迪克松定理
龐加萊一本迪克松定理 龐加萊一本迪克松定理
龐加萊一本迪克松定理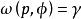 龐加萊一本迪克松定理
龐加萊一本迪克松定理 龐加萊一本迪克松定理
龐加萊一本迪克松定理 龐加萊一本迪克松定理
龐加萊一本迪克松定理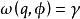 龐加萊一本迪克松定理
龐加萊一本迪克松定理 龐加萊一本迪克松定理
龐加萊一本迪克松定理(a) 假設且以為其極限集,即,則對於充分靠近且與p位於同側的點q,有,即為單側軌道漸近穩定的;
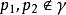 龐加萊一本迪克松定理
龐加萊一本迪克松定理 龐加萊一本迪克松定理
龐加萊一本迪克松定理 龐加萊一本迪克松定理
龐加萊一本迪克松定理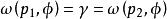 龐加萊一本迪克松定理
龐加萊一本迪克松定理 龐加萊一本迪克松定理
龐加萊一本迪克松定理(b) 假設,位於的不同側,且,則是軌道漸近穩定的(雙側) 。