矩陣
在數學中,矩陣(Matrix)是一個按照長方陣列排列的複數或實數集合,最早來自於方程組的係數及常數所構成的方陣。這一概念由19世紀英國數學家凱利首先提出。
矩陣是高等代數學中的常見工具,也常見於統計分析等套用數學學科中。在物理學中,矩陣於電路學、力學、光學和量子物理中都有套用;計算機科學中,三維動畫製作也需要用到矩陣。 矩陣的運算是數值分析領域的重要問題。將矩陣分解為簡單矩陣的組合可以在理論和實際套用上簡化矩陣的運算。對一些套用廣泛而形式特殊的矩陣,例如稀疏矩陣和準對角矩陣,有特定的快速運算算法。關於矩陣相關理論的發展和套用,請參考矩陣理論。在天體物理、量子力學等領域,也會出現無窮維的矩陣,是矩陣的一種推廣。
數值分析的主要分支致力於開發矩陣計算的有效算法,這是一個幾個世紀以來的課題,是一個不斷擴大的研究領域。 矩陣分解方法簡化了理論和實際的計算。 針對特定矩陣結構(如稀疏矩陣和近角矩陣)定製的算法在有限元方法和其他計算中加快了計算。 無限矩陣發生在行星理論和原子理論中。 無限矩陣的一個簡單例子是代表一個函式的泰勒級數的導數運算元的矩陣。
簡介
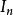 單位矩陣
單位矩陣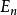 單位矩陣
單位矩陣主對角線上的元素都為1,其餘元素全為0的n階矩陣稱為n階單位矩陣,記為 或 ,通常用 I或 E來表示。
 單位矩陣
單位矩陣 單位矩陣
單位矩陣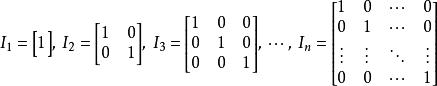 單位矩陣
單位矩陣線上性代數,大小為n的單位矩陣是在主對角線上均為1,而其他地方都是0的 的正方矩陣。它用 表示,或有時階數可忽略時就直接用 I來表示。如下所示:
同時單位矩陣也可以簡單地記為一個對角線矩陣:
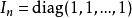 單位矩陣
單位矩陣性質
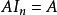 單位矩陣
單位矩陣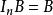 單位矩陣
單位矩陣根據矩陣乘法的定義,單位矩陣的重要性質為: 和
單位矩陣的特徵值皆為1,任何向量都是單位矩陣的特徵向量。
 單位矩陣
單位矩陣因為特徵值之積等於行列式,所以單位矩陣的行列式為1。因為特徵值之和等於跡數,單位矩陣的跡為 。
單位矩陣在高等代數中的套用
高等代數中,在求解相應的矩陣時若添加單位矩陣然後通過初等變換進行求解往往可以使問題變得簡單。
求等價標準型問題
設A是mxn矩陣,求A的等價標淮型D以及使PAQ=D成立的P與Q,按常規方法,一般會分別對A作行初等變化與列初等變化求出P、Q,而如果利用添加單位矩陣:即
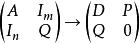 單位矩陣
單位矩陣當對A作行初等變換時,Im也作了相同的行初等變換,即化為P;
當對A作列初等變換時,In也作了相同的行初等變換,即化為Q。
求逆矩陣問題
設A是n階可逆矩陣,求其逆矩陣。
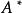 單位矩陣
單位矩陣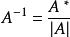 單位矩陣
單位矩陣一般的思想,同學們會先求出,再利用進行求解,這種方法算起來較麻煩且易出錯。
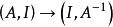 單位矩陣
單位矩陣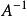 單位矩陣
單位矩陣可以利用,即把n階單位炬陣I在A的右邊,得到一個nx2n矩陣,然後對這一矩陣施行行初等變換,使得前n列變為I,這時後n列就化為了。
如果不知A是否可逆,也可用這種方法做,只要nX2n矩陣經行初等變換左邊的nxn那一塊中有一行(列)的元素全為0,則A不能經過初等變換化為單位矩陣,即A不可逆。
matlab 生成單位矩陣的方法
生成N為單位方陣
我們以N=5為例,生成5階單位方陣,在MATLAB主視窗中輸入 A=eye(5) 回車
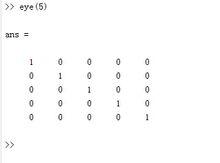 單位矩陣
單位矩陣特殊情況 eye和eye(1)
 單位矩陣
單位矩陣我們可以看到eye或者eye(1)生成的是標量1,也就是特殊的矩陣-1階單位方陣。

