簡介
 矩陣單位
矩陣單位 矩陣單位
矩陣單位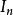 矩陣單位
矩陣單位 矩陣單位
矩陣單位 矩陣單位
矩陣單位線上性代數中,階 單位矩陣,是一個的方形矩陣,其主對角線元素為1,其餘元素為0。單位矩陣以表示;如果階數可忽略,或可由前後文確定的話,也可簡記為(或者E)。(在部分領域中,如量子力學,單位矩陣是以粗體字的 1表示,否則無法與作區別。)
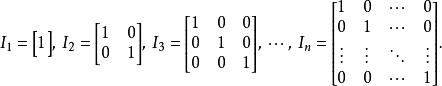 矩陣單位
矩陣單位 矩陣單位
矩陣單位 矩陣單位
矩陣單位一些數學書籍使用和(分別意為“單位矩陣”和“基本矩陣”),不過 I更加普遍。
 矩陣單位
矩陣單位 矩陣單位
矩陣單位 矩陣單位
矩陣單位特別是單位矩陣作為所有階矩陣的環的單位,以及作為由所有階可逆矩陣構成的一般線性群的單位元(單位矩陣明顯可逆,單位矩陣乘自己,仍是單位矩陣)。
 矩陣單位
矩陣單位 矩陣單位
矩陣單位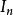 矩陣單位
矩陣單位這些階矩陣經常表示來自維向量空間自己的線性變換,表示恆等函式,而不理會基。
有時使用這個記法簡潔的描述對角線矩陣,寫作:
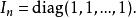 矩陣單位
矩陣單位也可以寫作克羅內克爾δ記法:
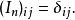 矩陣單位
矩陣單位克羅內克函式
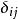 矩陣單位
矩陣單位在數學中, 克羅內克函式(又稱克羅內克δ函式、克羅內克δ)是一個二元函式,得名於德國數學家利奧波德·克羅內克。克羅內克函式的自變數(輸入值)一般是兩個整數,如果兩者相等,則其輸出值為1,否則為0。
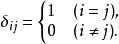 矩陣單位
矩陣單位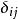 矩陣單位
矩陣單位克羅內克函式的值一般簡寫為。
克羅內克函式和狄拉克δ函式都使用δ作為符號,但是克羅內克δ用的時候帶兩個下標,而狄拉克δ函式則只有一個變數。
性質
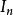 矩陣單位
矩陣單位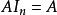 矩陣單位
矩陣單位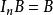 矩陣單位
矩陣單位根據矩陣乘法的定義,單位矩陣的重要性質為:且。
 矩陣單位
矩陣單位 矩陣單位
矩陣單位單位矩陣的特徵值皆為1,任何向量都是單位矩陣的特徵向量。具有重數。因為特徵值之積等於行列式,所以單位矩陣的行列式為1。因為特徵值之等於跡數,單位矩陣的跡為。
