解釋結構模型

套用圖的矩陣表示方法（見圖論）和簡單的邏輯運算，對複雜系統的各個組成元素（或子系統）間的結構關係加以描述的一種模型。英文縮寫為ISM。ISM通過對表示有向圖的相鄰矩陣的邏輯運算,得到可達性矩陣,然後分解可達性矩陣，最終使複雜系統分解成層次清晰的多級遞階形式。解釋結構模型在制訂企業計畫、城市規劃等領域已廣泛使用，尤其對於建立多目標、元素之間關係錯綜複雜的社會系統及其分析，效果更為顯著。

解釋結構模型

正文

　
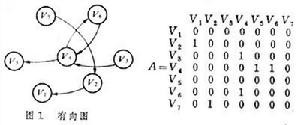
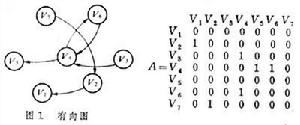用頂點Vi和Vj表示系統的元素(i=1,2,3…；j=1,2,3…。)，帶箭頭的邊【Vi Vj】表示兩元素之間的關係,即可構成有向圖（圖1）,用來表示有向圖中各元素間連線狀態的矩陣稱作相鄰矩陣A。當從Vi到Vj有帶箭頭的邊連線時,矩陣元素aij取值為1；無連線時取值為零。可達性矩陣M是用矩陣形式反映有向圖各頂點之間通過一定路徑可以到達的程度，它通過以下計算求得：將相鄰矩陣A加上單位矩陣I（矩陣中除主對角線上元素為1外，其餘元素皆為零的矩陣），然後用布爾代數規則 (0+0=0,0+1=1,1+1=1;0×0=0,0×1=0,1×1=1)進行乘方運算,直到兩個相鄰冪次方的矩陣相等為止。相等的矩陣中冪次最低的矩陣即為可達性矩陣。圖1所示有向圖的可達性矩陣M如下：通過對可達性矩陣的分解(有區域分解和級間分解)，即可建立系統的多級遞階結構模型（圖2）。多級遞階結構模型非常直觀清楚地反映了該系統元素之間的結構關係。ISM方法使用方便,不需要高深的數學理論，易為系統分析人員所掌握。

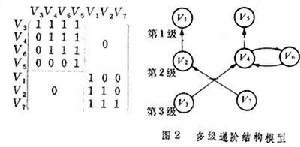解釋結構模型

參考書目
　汪應洛主編：《系統工程導論》,機械工業出版社,北京，1982。

配圖

相關連線