概念
初等變換有三種
(1)交換矩陣中某兩行(列)的位置;
(2)用一個非零常數k乘以矩陣的某一行(列);
(3)將矩陣的某一行(列)乘以常數k後加到另一行(列)上去。
三類初等矩陣都是可逆矩陣,即非奇異陣。
三類初等矩陣行列式的值是:
(1):-1
(2):k
(3):1
性質
 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣1、單位矩陣第i,j兩行互換得到的方陣為 ,將矩陣 的第i,j兩行互換所得矩陣 ,即有 = * 。
 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣說明:任意矩陣 的交換i,j行(列),取決於 是左乘 ,還是右乘 ,即: * 是交換行i,j變換, * 是交換列i,j變換。
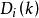 初等矩陣
初等矩陣 初等矩陣
初等矩陣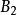 初等矩陣
初等矩陣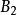 初等矩陣
初等矩陣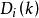 初等矩陣
初等矩陣 初等矩陣
初等矩陣2、單位矩陣第i行乘以常數k得到初等方陣 ,將矩陣 的第i行乘以k得到矩陣 ,即有 = * 。
 初等矩陣
初等矩陣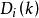 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣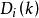 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣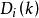 初等矩陣
初等矩陣 初等矩陣
初等矩陣說明:任意矩陣 的行(列)乘以常數k,取決於 是左乘 ,還是右乘 ,即 : * 是矩陣 行乘以常數k變換, * 是矩陣 列乘以常數k變換。
 初等矩陣
初等矩陣 初等矩陣
初等矩陣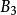 初等矩陣
初等矩陣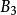 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣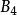 初等矩陣
初等矩陣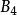 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣3、將單位矩陣的第i行的k倍加到第j行得到初等方陣 ,矩陣 的第i行的k倍加到第j行得到矩陣 ,即有 = * ;將單位矩陣的第j列的k倍加到第i列得到初等方陣 ,矩陣 的第j列的k倍加到第i列得到矩陣 ,即有 = * 。
 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣 初等矩陣
初等矩陣說明:任意矩陣 與初等矩陣相乘,表示對A進行初等變換,但對A進行的是行初等變換還是列變換,取決於初等矩陣 是左乘 ,還是右乘 ,即: * 是行初等變換,此時 的變換表示將 的第i行的k倍加到第j行(順序從前向後); * 是列初等變換,此時 的變換表示將 的第j列的k倍加到第i列(順序從後向前)。
套用
(1)在解線性方程組中的套用
初等行變換不影響線性方程組的解,也可用於高斯消元法,用於逐漸將係數矩陣化為標準形。初等行變換不改變矩陣的核(故不改變解集),但改變了矩陣的像。反過來,初等列變換沒有改變像卻改變了核。
(2)用於求解一個矩陣的逆矩陣
有的時候,當矩陣的階數比較高的時候,使用其行列式的值和伴隨矩陣求解其逆矩陣會產生較大的計算量。這時,通常使用將原矩陣和相同行數(也等於列數)的單位矩陣並排,再使用初等變換的方法將這個並排矩陣的左邊化為單位矩陣,這時,右邊的矩陣即為原矩陣的逆矩陣。

