簡介
數學上,高斯消元法(或譯:高斯消去法),是線性代數規劃中的一個算法,可用來為線性方程組求解。但其算法十分複雜,不常用於加減消元法,求出矩陣的秩,以及求出可逆方陣的逆矩陣。不過,如果有過百萬條等式時,這個算法會十分省時。一些極大的方程組通常會用疊代法以及花式消元來解決。當用於一個矩陣時,高斯消元法會產生出一個“行梯陣式”。高斯消元法可以用在電腦中來解決數千條等式及未知數。亦有一些方法特地用來解決一些有特別排列的係數的方程組 。
 圖1
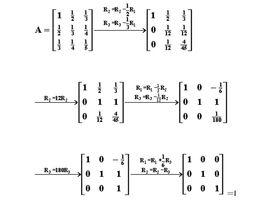
圖1Gauss-Jordan消元法在很多地方都會用到,例如求一個矩陣的逆矩陣、解線性方程組,等等。它的速度不是最快的,但是它非常穩定, 同時它的求解過程也比較清晰明了, 因而人們使用較多。相對於高斯消元法,Gauss-Jordan消元法最後的得到線性方程組更容易求解,它得到的是簡化行列式。其轉化後的增高矩陣形式如圖1所示,因此它可以直接求出方程的解,而無需使用替換算法。但是,此算法的效率較低。
G-J消元法的初等變換方法
G-J 消元法通過這樣的方法來進行初等變換:在每一個循環過程中,先尋找到主元,並將主元通過行變換 (無需列變換) 移動到矩陣的主對角線上, 然後將主元所在的行內的所有元素除以主元,使得主元化為 1;然後觀察主元所在的列上的其他元素,將它們所在的行減去主元所在的行乘以一定的倍數, 使得主元所在的列內、 除主元外的其他元素化為 0,這樣就使得主元所在的列化為了單位矩陣的形式。 這就是一個循環內做的工作。 然後, 在第二輪循環的過程中, 不考慮上一輪計算過程中主元所在的行和列內的元素, 在剩下的矩陣範圍內尋找主元, 然後(如果其不在主對角線上的話) 將其移動到主對角線上, 並再次進行列的處理, 將列化為單位矩陣的形式。 餘下的步驟依此類推。 具體的計算過程的一個例子, 請看下面求逆矩陣的過程的例子。
Gauss-Jordan 法的求解方程組的過程
引例
假設有如下的方程組:
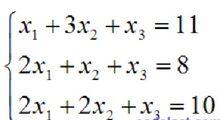 高斯-若爾當消元法
高斯-若爾當消元法寫成矩陣形式就是: AX=B ,其中:
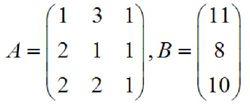 高斯-若爾當消元法
高斯-若爾當消元法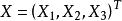 高斯-若爾當消元法
高斯-若爾當消元法且,現對矩陣 A 作初等變換,同時矩陣 B 也作同樣的初等變換,則當 A 化為單位矩陣的時候,有:
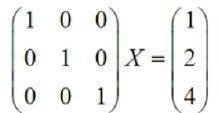 高斯-若爾當消元法
高斯-若爾當消元法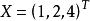 高斯-若爾當消元法
高斯-若爾當消元法顯而易見,我們得到了方程組的解:。
所以, 我們要以一定的策略, 對 A 和 B 施以一系列的初等變換, 當 A 化為單位矩陣的時候,B 就為方程組的解。
求解過程
如果要解係數矩陣相同、右端向量不同的 N 個方程組,在設計程式的時候,沒有必要 ”解 N次方程組 “,我們完全可以在程式中,將所有的右端向量以矩陣的數據結構(類似於二維數組)來表示, 在係數矩陣作行變換的時候, 矩陣里的每一個右端向量也做同樣的變換, 這樣,我們在一次求解運算的過程中,實際上就是同時在解 N 個方程組了。
用G-J消元法求逆
原理
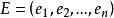 高斯-若爾當消元法
高斯-若爾當消元法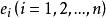 高斯-若爾當消元法
高斯-若爾當消元法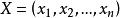 高斯-若爾當消元法
高斯-若爾當消元法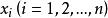 高斯-若爾當消元法
高斯-若爾當消元法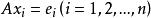 高斯-若爾當消元法
高斯-若爾當消元法 高斯-若爾當消元法
高斯-若爾當消元法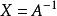 高斯-若爾當消元法
高斯-若爾當消元法假設 AX=E ,其中, A 為 n 階係數矩陣(與上面的解線性方程組對照);E 為單位矩陣,即,其中為單位列向量; X 為 n 個列向量構成的矩陣,即,其中為列向量。於是,可以把等式 AX=E 看成是求解 n 個線性方程組,求出了所有的之後,也即得到了矩陣 X。而由 AX=E 可知,矩陣 X 是 A 的逆矩陣,即。這樣,就求出了 A 的逆矩陣了。於是,求逆矩陣的過程被化成了解線性方程組的過程,因此我們可以用 Gauss-Jordan 消元法來求逆矩陣。求逆矩陣時,係數矩陣 A 和單位矩陣 E 可以共用一塊存儲區,在每一次約化過程中,係數矩陣逐漸被其逆矩陣替代。
示例
有如下的方程組:
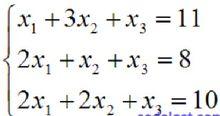 高斯-若爾當消元法
高斯-若爾當消元法顯而易見,該方程組對應的係數矩陣 A 和右端向量矩陣 B(此處只有一個右端向量)分別為:
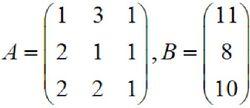 高斯-若爾當消元法
高斯-若爾當消元法其實在求逆矩陣的過程中,矩陣 B 無關緊要,可以忽略,不過此處還是把它寫出來了。下面,把單位矩陣 E 附在 A 的右邊,構成另一個矩陣(A|E):
 高斯-若爾當消元法
高斯-若爾當消元法下面,通過矩陣的初等變換,將 A 化為單位矩陣 E,而 E 則化為了 A 的逆矩陣。以下是轉化步驟:
(1)主元選為 3,所以將 Row1 (第一行)與 Row2 (第二行)交換:
 高斯-若爾當消元法
高斯-若爾當消元法(2)主元所在行的所有元素除以主元:
 高斯-若爾當消元法
高斯-若爾當消元法(3)Row1 – Row2 ,Row3 – 2 × Row2 :
 高斯-若爾當消元法
高斯-若爾當消元法現在,原來的矩陣 A 有一列被化為了單位陣的形式。
(4)重新選主元,這一次主元選為 5/3,於是 Row1 ÷ 5/3 (主元所在行的所有元素除以主元):
 高斯-若爾當消元法
高斯-若爾當消元法(5)Row2 – (1/3) × Row1 ,Row3 – (4/3) × Row1 :
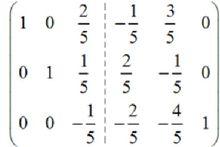 高斯-若爾當消元法
高斯-若爾當消元法現在,原來的矩陣 A 又有一列被化為了單位陣的形式。
(6)重新選主元,這一次主元選為 -1/5 ,於是 Row3 ÷ (-1/5) (主元所在行的所有元素除以主元):
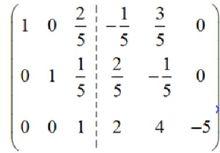 高斯-若爾當消元法
高斯-若爾當消元法(7)Row1 – (2/5) × Row3 ,Row2 – (1/5) × Row3 :
 高斯-若爾當消元法
高斯-若爾當消元法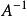 高斯-若爾當消元法
高斯-若爾當消元法現在,原來的矩陣 A 的所有列都被化為了單位陣的形式。可見,以上過程非常適合於計算機編程求解。至此,我們完成了從 A 到 E 的轉換,這個過程中使用了選主元的方法,但沒有使用列交換。於是,原來的單位矩陣 E 就變成了,即:
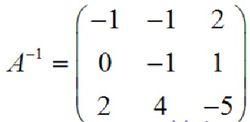 高斯-若爾當消元法
高斯-若爾當消元法