簡介
 質數和合數
質數和合數1.是兩個大於 1 的整數之乘積;
2.擁有某大於 1 而小於自身的因數(因子);
3.擁有至少三個因數(因子);
4.不是 1 也不是素數(質數);
5.有至少一個素因子的非素數。
以下是關於合數以及一些特殊合數的結論:
一個合數有奇數個因數(因子)若且唯若它是完全平方數。
基本概念
1.符合道理。《淮南子·兵略訓》:“發必中詮,言必合數,動必順時,解必中揍。”南朝梁劉勰《文心雕龍·體性》:“八體雖殊,會通合數,得其環中,則輻輳相成。”
2.數學用語。自然數中除能被1和本數整除外,還能被其他的數整除的數。如:6能被1和6整除,也能被2和3整除。
徐遲《哥德巴赫猜想》三:“老師說,你們都知道偶數和奇數,也都知道素數和合數。”
意義 一個數如果除了1和它本身以外還能被別的因數整除,這樣的數叫作合數。
基本概況
合數是指
①兩個數之間的最大公約數只是1的那兩個數的乘積;
②兩個數之間的公約數不只是1,用其中一個約數乘以最小的數,能整除,乘出來的那個數就是合數
合數又名合成數,是滿足以下任一(等價)條件的正整數:
1.是兩個大於1的整數之乘積;
2.擁有某大於1而小於自身的因數(因子);
3.擁有至少三個因數(因子);
4.不是1也不是素數(質數);
5.有至少一個素因子的非素數.
6、兩個或兩個以上素數的乘積,可以組成一個合數,並且只可以組成一個合數。反之,一個合數可以拆分為一組素數的乘積,並且只可以拆分為一組素數的乘積。也就是說:由三個以上素數的乘積組成的合數,不可以視為兩個素數的乘積!(也可以說除了1和它本身以外還有別的因數)
合數
1、1既不是質數也不是合數
2、一個合數,其約數除了1和它本身外還有其他
合數列
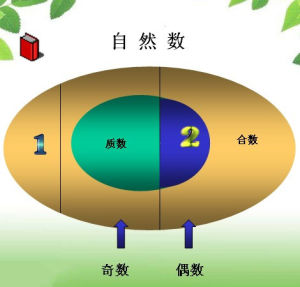
在自然數中,我們將那些可以被2整除的數叫作偶數,如2、4、6、8、10、...等,剩下的那些自然數就叫作奇數,如1、3、5、7、9、...等。這樣,所有的自然數就被分成了偶數和奇數兩大類。另一方面,除去1以外,有的數除了1和它本身以外,不能再被別的整數整除,如2、3、5、7、11、13、17、...等,這種數稱作素數(也稱質數)。有的數除了1和它本身以外,還能被別的整數整除,這種數就叫合數,如4、6、8、9、10、12、14、...等,就是合數。1這個數比較特殊,它既不算素數也不算合數。這樣,所有的自然數就又被分為1和素數、合數三類。類似4、6、8、9、10、12、14、...這個樣的數列叫做合數列
合數根和素數根
概念
除了2之外,所有的偶數都是合數。反之,除了2之外,所有的素數都是奇數。但是奇數包括了合數和素數。合數根和素數根的概念就是用來區分任何一個大於9的奇數屬於合數還是素數。任何一個奇數都可以表示為2n+1(n是非0的自然數)。我們將n命名為數根。當2n+1屬於合數時,我們稱之為合數根;反之,當2n+1是素數時,我們稱之為素數根。規律
任何一個奇數,如果它是合數,都可以分解成兩個奇數的乘積。設2n+1是一個合數,將它分解成兩個奇數2a+1和2b+1的積(其中a、b都屬於非0的自然數),則有2n+1=(2a+1)(2b+1)=4ab+2(a+b)+1=2(2ab+a+b)+1可見,任何一個合數根都可以表示為"2ab+a+b",反之,不能表示為"2ab+a+b"的數根,就稱為素數根。由此可以得到合數根表。判斷一個大奇數屬於合數還是素數,只需在合數根表中查找是否存在它的數根就知道了。合數根表
表中第一行表示a的取值,第一列表示b的取值,其餘表示2ab+a+b| 2ab+a+b | a=1 | a=2 | a=3 | a=4 | a=5 | a=6 | a=7 | a=8 | a=9 | a=10 | … | a=n |
| b=1 | 4 | 7 | 10 | 13 | 16 | 19 | 22 | 25 | 28 | 31 | … | 1+3n |
| b=2 | 7 | 12 | 17 | 22 | 27 | 32 | 37 | 42 | 47 | 52 | … | 2+5n |
| b=3 | 10 | 17 | 24 | 31 | 38 | 45 | 52 | 59 | 66 | 73 | … | 3+7n |
| b=4 | 13 | 22 | 31 | 40 | 49 | 58 | 67 | 76 | 85 | 94 | … | 4+9n |
| b=5 | 16 | 27 | 38 | 49 | 60 | 71 | 82 | 93 | 104 | 115 | … | 5+11n |
| b=6 | 19 | 32 | 45 | 58 | 71 | 84 | 97 | 110 | 123 | 136 | … | 6+13n |
| b=7 | 22 | 37 | 52 | 67 | 82 | 97 | 112 | 127 | 142 | 157 | … | 7+15n |
| b=8 | 25 | 42 | 59 | 76 | 93 | 110 | 127 | 144 | 161 | 178 | … | 8+17n |
| b=9 | 28 | 47 | 66 | 85 | 104 | 123 | 142 | 161 | 180 | 199 | … | 9+19n |
| b=10 | 31 | 52 | 73 | 94 | 115 | 136 | 157 | 178 | 199 | 220 | … | 10+21n |
| …… | … | … | … | … | … | … | … | … | … | … | … | …… |
| b=n | 1+3n | 2+5n | 3+7n | 4+9n | 5+11n | 6+13n | 7+15n | 8+17n | 9+19n | 10+21n | … | n^2+2n |