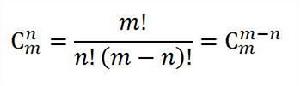組合數

從n個不同元素中，任取m(m≤n)個元素並成一組，叫做從n個不同元素中取出m個元素的一個組合；從n個不同元素中取出m(m≤n)個元素的所有組合的個數，叫做從n個不同元素中取出m個元素的組合數。

基本信息

• 中文名：組合數
• 英文名：combinatorial number

• 中文名：組合數
• 英文名：combinatorial number

• 所屬學科：數學
• 公式：C(n,m)=n!/((n-m)!*m!)（m≤n）
• 性質1：C(n,m)= C(n,n-m)
• 性質2：C(n,m)=C(n-1,m-1)+C(n-1,m)
• 參考資料：《數學辭海》第1卷

定義

組合數

組合是數學的重要概念之一。從 n 個不同元素中每次取出 m 個不同元素 ，不管其順序合成一組，稱為從 n 個元素中不重複地選取 m 個元素的一個組合。所有這樣的組合的種數稱為組合數。

計算公式

線上性寫法中被寫作C(n,m)。

組合數的計算公式為

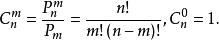組合數

組合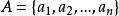數

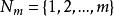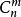組合數

組合數

n 元集合 A 中不重複地抽取 m 個元素作成的一個組合實質上是 A 的一個 m 元子集和。如果給集 A 編序 成為一個序集，那么 A 中抽取 m 個元素的一個組合對應於數段 到序集 A 的一個確定的嚴格保序映射。組合數 的常用符號還有

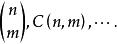組合數

性質

互補性質

1.

互補性質

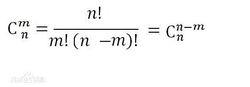組合數

即從 n個不同元素中取出 m個元素的組合數=從 n個不同元素中取出 ( n-m) 個元素的組合數；

這個性質很容易理解，例如C(9,2)=C(9,7)，即從9個元素里選擇2個元素的方法與從9個元素里選擇7個元素的方法是相等的。

規定：C(n,0)=1 C(n,n)=1 C(0,0)=1

2.組合恆等式

若表示在 n 個物品中選取 m 個物品，則如存在下述公式：C(n,m)=C(n,n-m)=C(n-1,m-1)+C(n-1,m)。