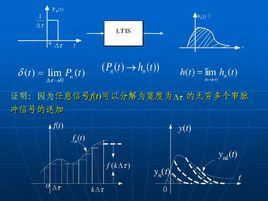
定義
卷積與傅立葉變換有著密切的關係。以(x) ，(x)表示L1（R）1中f和g的傅立葉變換，那么有如下的關係成立：（f *g）∧（x）=(x)·(x)，即兩函式的傅立葉變換的乘積等於它們卷積後的傅立葉變換。這個關係，使傅立葉分析中許多問題的處理得到簡化。
由卷積得到的函式（f *g）（x），一般要比f，g都光滑。特別當g為具有緊支集的光滑函式，f 為局部可積時，它們的卷積（f *g）（x）也是光滑函式。利用這一性質，對於任意的可積函式 ， 都可以簡單地構造出一列逼近於f 的光滑函式列fs（x），這種方法稱為函式的光滑化或正則化。
卷積的概念還可以推廣到數列 、測度以及廣義函式上去。
由來
學習 信號與系統必須貫穿一個核心的思想，那就是信號分解的思想 。看到一個很複雜的信號，我們往往是無從下手的，這個時候若能把複雜的信號進行分解，分解成我們常見的信號，複雜信號的分析過程自然就演變成了對簡單信號的分析 。也就是說我們只需要掌握一些比較典型的簡單信號的特性，而剛好一些複雜的信號都可以表示成這些簡單信號的組合，那么我們就可以實現複雜信號的分析，卷積積分的思想就源自於此。
那么到底什麼樣的簡單信號可以表示複雜信號呢？其實如果這個問題能夠回答好的，信號與系統的核心問題就解決了 。對時域而言，對於連續信號，單位衝激信號就可以實現這樣的功能，於是通過推導和演變，就引出了卷積積分的定義式 。在頻域，是把複雜的信號表示成不同頻率的正弦信號的線性組合，於是就引出了信號的傅立葉變換，離散信號同樣如此。
任意連續信號可以分解成單位衝激信號的線性組合， 也就是說任意連續信號都可以分解成不同強度的衝激信號的線性疊加，對於不同的信號而言，分解的形式都是相同的，不同僅僅是 f(τ)這樣的一個積分形式即定義為卷積積分。
意義
任何信號 都可以表示成信號本身和單位衝激信號的卷積，展開就是卷積積分的形式，不同的信號都可以分解成相同的形式，那么這個過程就簡化了分析。 另外，當分析信號作用系統的回響時，對於任意信號作用於某個衝激回響為 的LTI系統而言，利用疊加性和均勻性就可以得到其輸出的零狀態回響。最後可以得到的結論是系統的零狀態回響是輸入信號和系統的單位衝激回響的卷積積分 。利用這樣的一種卷積積分的方法來求系統的零狀態回響較之經典的時域分析法要簡單很多，而且物理含義也比較明確。
物理意義
在激勵條件下，線性電路在t時刻的零狀態回響=從激勵函式開始作用的時刻（ξ=0）
到t時刻（ ξ=t）的區間內，無窮多個強度不同的衝激回響的總和。
可見，衝激回響在卷積中占據核心地位。
機率意義
機率論中，兩個相互獨立的隨機變數變數X與Y的和的機率密度函式是X與Y的機率密度函式的卷積。
計算方法
卷積積分 在時域分析中是一個很重要的概念和數學工具。除了卷積的圖解法和數值解以外 ，直接根據卷積定義的函式式求積分也可以採用幾種不同的方來進行 。
現以圖1 所示兩個波形為例, 用下述不同方法求解f(t) *g(t)。
卷積積分分段卷積法求解
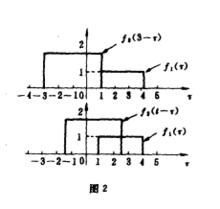
求 上列兩函式的卷積時,可分為圖2 所求5個區間來進行。
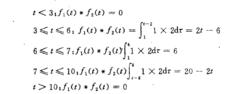卷積積分
卷積積分 卷積積分用此法進行卷積積分,數學概食清楚,函式計算式簡單,藉助於一定的圖形,卷積的物理含義亦十分清晰。在每段時間域中f1(t)*f2(t)與t的函式關係一目了然。它適用於任何兩個信號的卷積積分計算。間題就是對初學者積分的上、下限不易正確確定。通常,在每個分段時間域中,若函式f1( )和f2(t- )兩波形的後沿值(即函式不為零的最小值)分別為tr1和tr2,兩波形前沿值(即函式右邊界
卷積積分的最大r值)分別為tr1和tr2,則積分的下限應取它們後沿值中的最大者,即max〔tr1,tr2〕,積分上限取它們前沿值中的最小者,即min〔tr1,tr2〕。
闡門函式法求解
可將 上列函式分別表示為
f1(t)=v(t-1)-v(t-4)
f2(t)=2[v(t-2)-v(t-6)]
由此得:
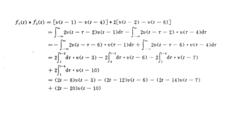卷積積分 卷積積分 卷積積分這種種卷積方法用一個函式表達式可將結果全部表示出來,且根據各個積分的被積函式v(t- -t1)·v( 一t0)所確定的門限,很容易將門的上、下限分別確定為積分的上限(t一t1)、下限(t0),積分後各函式的定義域的下限只要由積分的上限減去下限(t一t1一t0)後即可確定。因此該方法容易理解和掌握,尤其對初學者很容易接受。它除了適用廠於上列分段函式的卷積分外,還可適用於連續函式波形。
用卷積的徽、積分性質求解
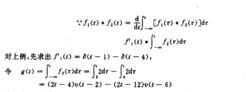卷積積分由於 衝激函式與任何函式的卷積積分皆為該函式本身,因此很快可求出
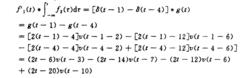卷積積分
卷積積分 卷積積分 卷積積分 卷積積分
卷積積分 卷積積分用該性質求卷積,可避免複雜的積分運算,同時也避免了確定積分限的問題,它非常適合於兩函式中一個為階躍信號或斜坡信號或可用階躍信號的組合來表示的折線信號,由於u'(t)= (t)(或[tv(t)])”=(t)而f(t)*(t)=f(t),由此計算自然會簡化一些.但是該方法的套用有一定的限制,它必須要求f1(- )=f2(- )=0.另外,如果不合理地亂加套用,比如對一信號求導,而對另一信號的積分並不容易,則使得整個計算並不簡單,或許還會計算出錯誤的結果.
利用時移性質求解
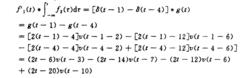卷積積分設
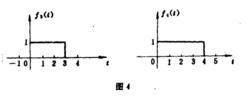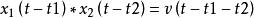卷積積分
卷積積分則
用此性質,可將上列兩波形先移至如圖4所示的位里,分別用f3(t)和f4(t)來表示:
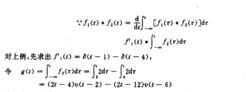卷積積分再由卷積的線性性：
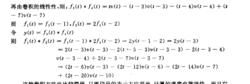卷積積分這種卷積方法也比較簡便,只要信號的表示方法得當,計算的速度也就很快。而且它
對連續函式亦適用。
上面對同一例題,用4種不同方法對卷積積分進行了計算。這些常用方法對我們在信號與系統課程中所遇到的絕大部分信號的卷積計算都是適用的(除參予卷積的兩信號中有一為衝激信號,可直接進行計算,不必再用2、3、4方法)。通過比較還可知,分段卷積法最直接明了,但其它三種方法都比較容易接受和掌握。
套用
在 電路分析中要求解任意激勵的零狀態回響時，可採用卷積積分法和拉普拉斯變換法，現分別敘述如下：（1）卷積積分法已知電路的衝激回響為h（t），則任意激勵e（t）的零狀態回響r（t）求得拉普拉斯變換法（也稱運算法）①先將表示電壓或電流的時域形式的任意激勵f（）做拉氏變換，得到復頻域的電壓或電流激勵的象②從等效運算電路求解以象函式為變數的線性代數方程，得到電壓或電流回響的象函式。③再利用拉氏反變換（通常可以查表）求原函式，即可得任意激勵e（t）的時域形式的零狀態回響。
在 電路分析中,套用卷積積分時,首先要找到單位衝激回響,這是在電路分析中正確套用卷積積分的關鍵所在,而單位衝激回響可以通過網路函式的反拉氏變換求得.一般對應的網路函式求解較為方便。那么給定的任何激勵的零狀態回響都可以通過卷積積分求得.如果網路處於非零狀態,則全回響把上敘結果加上零輸入回響即為所求.
