光學信息處理
正文
“信息”是通信科學中早就採用的術語,例如一個受調製的電信號(電壓或電流波)可看作攜帶著信息的隨時間變化的序列。這個觀點也適用於光學,例如一幅圖像實際上是一種二維空間的光強或光場分布,它可以看作攜帶著信息的光強或光場隨空間變化的序列,稱為光學信息。光學信息可以是一維的、或二維、三維的空間性的信息。近年來發展起來了“信息光學”的近代光學分支,它包含光學傳遞函式、全息術、光學信息處理等各部分的理論和實踐。光學信息處理是在傅立葉光學基礎上發展起來的。它研究如何對各種光學信息進行綜合性的處理。例如各種光學運算(加、減、乘、除、相關、卷積、微分、矩陣相乘、邏輯運算等);光學信息的抽取、編碼、存儲、增強、去模糊、特徵識別;各種光學變換(傅立葉變換、對數變換、梅林變換、拉普拉斯變換)等。有時光學信息處理也稱為光學數據處理,它的發展遠景是“光計算”。
實際上,相乾光處理系統是一個光學模擬計算機,它具有二維並行處理的能力,極高的運算速度(光速),以及極大的容量等。這些都是目前數字計算機難以達到的。目前由於某些器件如實時空間光調製器發展未趨完善,限制了運算速度。還有,目前光學處理的精度較低,靈活性較差,使它在套用上受到了一定的限制。
光學信息處理有許多種類。按處理的性質可分為線性處理和非線性處理兩大類。線上性處理中又分為空間不變和空間可變兩類。按所用光的相干性可分為相干、非相干和部分相干處理等類。
線性處理 所謂線性處理是指系統對多個輸入之和的回響(即輸出)等於各單獨輸入時的回響(輸出)之和。一個光學成像系統就是典型的線性系統。
在相干光照明時,光學透鏡所具有的傅立葉變換性質也是一種線性的性質。光學透鏡將不同的光學圖像變換成不同的空間頻譜。可以用光電探測元件接收各個部分的空間頻譜來進行分析。近代一些採用光電結合的空間頻譜分析儀是根據上面介紹的原理製成的,它可用到遙感圖像、醫學圖像分析等方面。下面介紹一些線性的光學濾波處理。
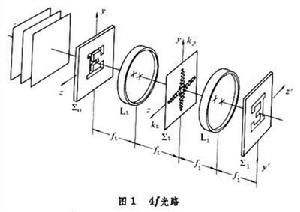
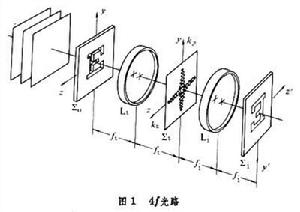
如圖1所示,在E字的空間頻譜面後面再置放一個與Lt 相同的變換透鏡Li,頻譜位於Li的前焦面上(頻譜面上不要置放任何螢幕)。這樣,Li對於頻譜面上的圖像又進行一次傅立葉變換而在Li的後焦面上得到了原圖像 E字的倒像。這樣的光學系統稱為4f光學系統,是一種典型的光學信息處理系統。如用一個半透明或不透明的小屏置於Σt頻譜面上的零頻和低頻部分,可削弱或擋住這些零頻和低頻部分,而讓高頻部分通過,在Σi面上便可得到邊緣增強的 E字圖像。這實際上是在頻譜面上抽取了較高空間頻率的圖像信息再經透鏡Li的傅立葉變換而形成了新的圖像,稱為空間濾波法。這裡介紹的是一種相干光線性運算或處理。使用不同的濾波片可進行不同的濾波處理(高通、低通、帶通、方向濾波、複數濾波等)以提取不同的信息,使各種輸入圖像得到相應的變化。
 光學信息處理
光學信息處理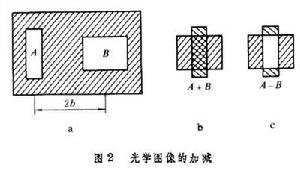 光學信息處理
光學信息處理光學圖像的加減是光學信息處理中的重要基本運算方法之一,它也是微分運算、邏輯運算的基礎。光學圖像的相減也可直接套用來提取兩個不同圖像的差異信息,例如同一地區在不同時刻的兩個“雲圖”間的差異等。近代已研究了多種多樣的光學相加和相減法。
光學圖像的特徵識別是指在一幅輸入圖像中找出某已知特徵圖像的光學處理方法。設已知特徵圖像的光場透射函式為g(x,y),可以用拍攝g(x,y)的傅立葉變換全息圖的方法來製成一個復空間濾波器G*,G*是已知特徵圖像g(x,y)的空間頻譜G的複數共軛,這種濾波器稱為已知特徵圖像的匹配濾波器。在通信技術中使用時域匹配濾波器可檢測埋在相加性噪聲中的已知信號,現在使用的是用全息方法製成的含有G*信息的空間匹配濾波器。當把輸入圖像f(x,y)=g(x,y)+“噪聲”(這裡“噪聲”包括輸入圖像中除了特徵圖像之外的其他圖像) 放在4f相干光處理系統的輸入平面∑0上, 如果在 ∑t上放上匹配濾波器G*,則已知特徵圖像g(x,y)的頻譜G 經空間匹配濾波器G*調製後的光場可表為
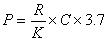 ,再經Li變換透鏡後在輸出平面上可得到具有很高峰值的亮斑(g的自相關函式);而輸入圖像的“噪聲”部分與g(x,y)形成互相關函式,一般表現沒有明顯峰值分布。這種利用匹配濾波器進行相關運算過程可以圖3的位相補償原理來說明。從相干光源來的平面波陣面透過輸入函式f(x,y)後產生畸變〔由g(x,y)和“噪聲”兩者引起〕,其中對應於已知特徵圖像g(x,y)的畸變波陣面在濾波面上變為G,經匹配濾波G*調製得到了位相補償的|G|2,恢復為平面波陣面,經Li會聚在輸出平面∑i上形成一亮斑,即特徵圖像g(x,y)的自相關輸出,由亮斑位置可以確定特徵圖像在輸入圖像中的位置。由於“噪聲”所引起的畸變波陣面,不能從濾波器得到位相補償,不能恢復成為平面波陣面,互相關輸出在輸出平面上不能形成亮斑。以上這種特徵識別方法,在圖像識別和分類,從噪聲中檢測電信號(如雷達、聲吶的回波)等方面得到套用。綜合孔徑雷達數據的光學處理是光學信息處理中最早最成功的套用。
,再經Li變換透鏡後在輸出平面上可得到具有很高峰值的亮斑(g的自相關函式);而輸入圖像的“噪聲”部分與g(x,y)形成互相關函式,一般表現沒有明顯峰值分布。這種利用匹配濾波器進行相關運算過程可以圖3的位相補償原理來說明。從相干光源來的平面波陣面透過輸入函式f(x,y)後產生畸變〔由g(x,y)和“噪聲”兩者引起〕,其中對應於已知特徵圖像g(x,y)的畸變波陣面在濾波面上變為G,經匹配濾波G*調製得到了位相補償的|G|2,恢復為平面波陣面,經Li會聚在輸出平面∑i上形成一亮斑,即特徵圖像g(x,y)的自相關輸出,由亮斑位置可以確定特徵圖像在輸入圖像中的位置。由於“噪聲”所引起的畸變波陣面,不能從濾波器得到位相補償,不能恢復成為平面波陣面,互相關輸出在輸出平面上不能形成亮斑。以上這種特徵識別方法,在圖像識別和分類,從噪聲中檢測電信號(如雷達、聲吶的回波)等方面得到套用。綜合孔徑雷達數據的光學處理是光學信息處理中最早最成功的套用。 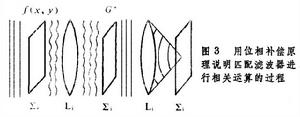 光學信息處理
光學信息處理如果一個線性系統的脈衝回響函式隨輸出點的位置而改變,則該系統稱為線性空間可變系統。這時上述的傅立葉頻域處理方法就不再能適用,必需要尋找另外的處理方法。其中一種方法是先對於輸入圖像進行某種坐標變換,然後在傅立葉頻域內進行空間不變濾波運算,最後再經過某種坐標變換(有時可省去這一變換),得到輸出圖像。坐標變換可以用全息圖、計算全息圖或非線性圖像掃描裝置等方法來實現。下面舉出一個線性空間可變光學信息處理的例子,即比例不變特徵識別。
在上例中的輸入函式g(x,y)如果在尺寸上發生了變化,即g(x,y)變為g(ax,ay),a表示一個任意正實數,也就是說g(x,y)被放大或縮小,那么它的傅立葉變換空間頻譜G的尺寸也相應地縮小或放大。但這時匹配濾波器上G*卻是固定不變的,所以便不能夠很好地校正G的畸變位相而進行特徵識別。如何對於比例變化的特徵圖像進行有效的匹配濾波識別,這要求尋找一種變換,它對於任何比例的一種特徵圖像(例如某人的指印圖紋採取不同的比例放大或縮小)的空間變換頻譜的尺寸是一樣的。這種變換就是所謂梅林變換。對不同比例的一種特徵圖像g(x,y)進行梅林變換,可以證明空間梅林頻譜G都是相同的,這樣便可以用同一個匹配濾波器G*來校正G的位相畸變。
可以證明,對一個函式g(x,y)先進行對數坐標變換,然後再進行傅立葉變換,便可得到該函式的梅林變換。可以用圖4的光路來實現對數坐標變換。g(ax,ay)表示輸入函式,用相干平行光照明,輸入函式後面緊貼放置一片含有透射率函式
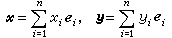 的計算全息圖片,再經過傅立葉變換透鏡後,在其後焦面上得到輸出。根據不同需要的輸出,可以計算出來所需的═(x,y),從而設計研製出來相應的計算機全息圖放在輸入平面上,作為一種位相濾波器以得到某種坐標變換(例如對數坐標變換等)的輸出。圖5表示將已獲得的對數變換圖片 g(eu,eu,)作為傳統的4f系統(線性空間不變系統)的輸入圖像,經Lt變換後得到G,再經過匹配濾波器G*校正其位相畸變,然後在輸出平面上形成相關峰值的亮斑,這就實現了比例不變光學圖像模式識別。它是一種線性空間可變光學信息處理。它包括兩步:第一步是對於輸入圖像進行對數變換,第二步是將經過對數變換後的圖像在傳統的4f系統中進行空間不變匹配濾波運算。
的計算全息圖片,再經過傅立葉變換透鏡後,在其後焦面上得到輸出。根據不同需要的輸出,可以計算出來所需的═(x,y),從而設計研製出來相應的計算機全息圖放在輸入平面上,作為一種位相濾波器以得到某種坐標變換(例如對數坐標變換等)的輸出。圖5表示將已獲得的對數變換圖片 g(eu,eu,)作為傳統的4f系統(線性空間不變系統)的輸入圖像,經Lt變換後得到G,再經過匹配濾波器G*校正其位相畸變,然後在輸出平面上形成相關峰值的亮斑,這就實現了比例不變光學圖像模式識別。它是一種線性空間可變光學信息處理。它包括兩步:第一步是對於輸入圖像進行對數變換,第二步是將經過對數變換後的圖像在傳統的4f系統中進行空間不變匹配濾波運算。 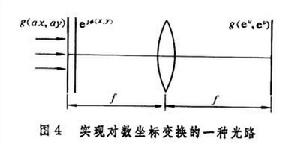 光學信息處理
光學信息處理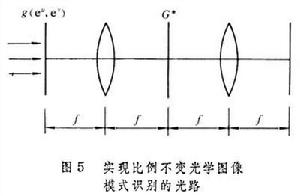 光學信息處理
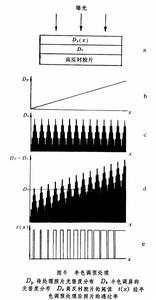
光學信息處理非線性處理 在實際問題中常會遇到一些線性處理無法解決的問題。例如,如何突出圖像中某一灰度等級,怎樣從相乘性噪聲中提取信號,傅立葉光學對這些問題變得無能為力了。因為這些問題都是非線性問題,所謂非線性系統是指輸出圖像的光強不再與輸入圖像光強保持正比關係。為了實現非線性處理,可以在光學系統中放入非線性光學元件,或者先通過預處理方法實現某種非線性變換,再由線性系統濾波處理。照相膠片就是一種非線性元件,利用膠片感光特性曲線的非線性,控制對襯度(γ值),可實現正、負冪次非線性關係。另一類非線性元件是非線性光學材料。例如可飽和吸收介質、光色材料、電光晶體等在強光下的非線性行為可用在頻域或空域進行諸如閾值控制等非線性處理,但這些方法都不夠靈活。目前靈活性最大的方法是半色調預處理方法。所謂半色調預處理方法來自印刷製版技術,通過半色調屏(又稱網屏,是一維或二維周期結構的柵網,在每個周期內灰度分布呈階梯形或其他分布)對圖象進行翻拍,如圖6所示,利用高反襯度膠片的限幅性質,把連續色調圖像變為由點陣(二維)或線陣(一維)組成的黑白兩種色調的照片,稱為“半色調照片”。原圖像中灰度信息轉變為半色調照片中不同面積的點陣(二維)或不同寬度的線陣(一維),這種預處理過程相當於通信論中對連續函式信號進行脈衝寬度調製,這個過程實現了第一個非線性變換,然後把半色調照片放線上性光學處理系統中,在濾波平面用小孔選取不同衍射級次,在輸出平面上實現第二個非線性變換,使輸出光強非線性地依賴於脈寬,從而也非線性地依賴於原圖像灰度等級。設計不同類型的半色調屏,將能實現不同的非線性變換。
 光學信息處理
光學信息處理 光學信息處理
光學信息處理 光學信息處理
光學信息處理 光學信息處理
光學信息處理 光學信息處理
光學信息處理 光學信息處理
光學信息處理 光學信息處理
光學信息處理近年來,由於其他學科的滲透,在光學信息處理領域中出現一些新的發展方向。例如利用光學反饋概念線上性和非線性運算方面取得一些新結果;利用光學雙穩態現象有可能在半導體材料上製成一種新型信息處理元件,有可能成為未來光計算機的運算元件;四波混頻及其共軛位相已用來恢復經過位相介質畸變了的圖像,以及一種新的光學元件──位相共軛元件將在多方面得到套用;聲表面波器件與集成光學相結合有可能成為光通信中新的處理元件,並在雷達等信號處理中發揮重要作用;此外人們已開始考慮時間(一維)與空間(三維)相結合的四維處理系統。最後應該指出的是,把光學處理的二維、高速、空間頻寬積大等長處與電子計算機數字處理的靈活性和高精度相結合成光電混合處理系統,將是一個完善和有實用價值的系統。
參考書目
H. Stark, ed., Applications of Optical Fourier Transforms, Academic Press, New York, 1982.