圓周卷積

點信號，其中，則它們的圓周卷積就與卷積相等。 x[n x[n

定義

x(t) 的周期延伸可以寫成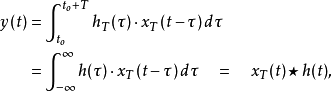
x_T(t) \ \stackrel{\mathrm{def}}{=} \ \sum_{k=-\infty}^{\infty} x(t - kT) = \sum_{k=-\infty}^{\infty} x(t + kT).兩個函式 x(t) 與 h(t) 的圓周卷積 x(t) \otimes h(t)可用兩種互相等價的方式來定義
\begin{align}y(t) &= \int_{t_o}^{t_o+T} h_T(\tau)\cdot x_T(t - \tau)\,d\tau \\&= \int_{-\infty}^{\infty} h(\tau)\cdot x_T(t - \tau)\,d\tau\quad = \quad x_T(t) \star h(t),\end{align}
其中\star表示原本的（線性）卷積。
類似的，對於離散信號（數列），可以定義周期 N 的圓周卷積x[n] \otimes h[n]為
\begin{align}x_N[n] \star h[n] &= \sum_{m=-\infty}^{\infty} h[m] \cdot x_N[n-m] \\&= \sum_{m=-\infty}^{\infty} h[m] \cdot \sum_{k=-\infty}^{\infty} x[n -m -kN].\,\end{align}

算法

離散信號的圓周卷積可以經由圓周卷積定理使用快速傅立葉變換（FFT）而有效率的計算。因此，若原本的（線性）卷積能轉換成圓周卷積來計算，會遠比直接計算更快速。考慮到長度L和長度 M 的有限長度離散信號，做卷積之後會成為長度L+M-1的信號，因此只要把兩離散信號補上適當數目的零（zero-padding）成為 N 點信號，其中N\ge L+M-1\,，則它們的圓周卷積就與卷積相等。即可接著用 N 點 FFT 作計算。
用以上方法計算卷積時，若兩個信號長度相差很多，則較短者須補上相當多的零，太不經濟。而且在某些情況下，例如較短的 h[n] 是一個 FIR 濾波器而較長的 x[n] 是未知長度的輸入（像語音）時，直接用以上方法要等所有的輸入都收到後才能開始算輸出信號，太不方便。這時可以把 x[n] 分割成許多適當長度的區塊（稱為 block convolution），然後一段一段的處理。經過濾波後的段落再仔細的連線起來，藉由輸入或輸出的重疊來處理區塊連線的部份。這兩種做法分別稱為重疊-儲存之卷積法和重疊-相加之卷積法。

相關詞條

熱門詞條

聯絡我們