剛體定點轉動解法
剛體繞固定點的純慣性運動 即外力矩為零時剛體的運動。具有迴轉對稱慣性橢球的剛體 這種剛體的純慣性運動具有較簡單的形態:規則進動。此時剛體等速地繞迴轉對稱軸自轉,而迴轉軸又對空間固定的某軸(即L)軸)以不變的張角作等速轉動。剛體的運動就象是同剛體固連的本體極錐從空間極錐無滑動地滾過所形成的運動（見剛體定點轉動）。滾動的情況分為外接和內接兩種，分別如圖1和圖2所示。 一般情況下的剛體 這種剛體繞固定點的純慣性運動可用分析法或幾何法求解。
① 分析法 可用雅可比橢圓函式給出表示剛體位置的嗞、θ、ψ 的分析解。這種剛體運動有兩個第一積分：
能 量 積 分 ,
動量矩積分 ,
式中Ixx、Iyy、Izz分別為剛體繞x軸、y軸、z軸的轉動慣量;ωx、ωy、ωz別為剛體繞x 軸、y軸、z軸的角速度；T 為動能；L 為動量矩的大小。不失一般性，可以假定Ixx＞Iyy＞Izz。對這種剛體的任意非零運動狀態恆有Ixx＞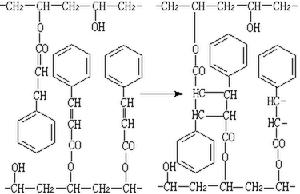
＞Izz成立。利用上述兩個第一積分,消去變數ωx、ωz,若初始條件滿足(對的情形可作類似討論)，由歐拉動力學方程（見剛體動力學）可得： 
,
,
,
。
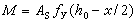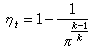積分上式，得到： 式中t0是u=0（亦即ωy=0）的時刻。由此可見,u作為時間t的函式是一個典型的代數函式積分的反轉。按照雅可比的定義，這個反轉是如下的橢圓函式：。
求得ωy之後，代入第一積分，即可得出用橢圓函式表示的ωx、ωy、ωz：,
,
,
式中，
，
。
為求得剛體每時刻的角位置,假定取空間固定的z軸為不變的動量矩L的方向，則有：，
，
，
由此得到：，
，
這就決定了嗞,θ 為時間的函式。求ψ可利用運動學公式，
從而得到：。
② 幾何法 以上的結果，從分析上來說是徹底的，但L.潘索的幾何解法卻能更形象地描繪出這個問題中剛體運動的直觀圖案。這種幾何解法是以剛體繞固定點轉動的幾個一般性質為依據的：選定慣性橢球常數k=1,稱剛體瞬時角速度ω的方向線和橢球的交點O1為極點，則橢球在極點的切平面必和動量矩矢量L垂直；固定點O到極點切平面的距離在剛體繞固定點的純慣性運動中，有如下兩個守恆律：動量矩矢量的大小和方向不變;動能T不變。由此可以斷定，慣性橢球在極點的切平面是一個不變平面。剛體繞固定點的純慣性運動，可以形象地看成是隨著慣性橢球在此不變平面上無滑動地（由於極點恆在瞬時轉軸上，速度為零）滾過而產生的運動,如圖3所示。滾動時極點在橢球上留下的軌跡是本體極跡,在不變平面上留下的軌跡是空間極跡。圖4和圖5是表示極跡的典型圖像。剛體繞慣性主軸的運動最為簡單，這種純慣性運動可以使鏇轉不變地保持下去，稱為永久轉動。可以證明，永久轉動的轉軸一定是慣性主軸。從圖4中可以看出，三個永久轉動鄰近的極跡並不相似，這種區別反映了永久轉動穩定性不同。剛體繞橢球長軸和短軸的永久轉動是穩定的，繞中間軸的永久轉動是不穩定的。 剛體繞固定點的受迫運動 這種運動表現的形態一般較為複雜。但在特殊情況下，即剛體的慣性橢球迴轉對稱，初始條件有繞迴轉軸的高速自轉，從而具有大的自轉動量矩，剛體繞固定點的受迫運動呈現較簡單的陀螺運動規律。對這種運動的研究首先是從對天文學上的歲差和章動等現象的研究開始的。歲差和章動的實質是：地球作為一個巨大剛體，在作軌道運動和自轉運動的同時,還有繞地心的複雜的角運動。通過計算各個天體(日、月、行星)對地球的作用力矩,可精確地計算出地軸的受迫運動。這種運動表現為進動和章動。地球除繞地軸自轉外,還以23°27┡為半張角的圓錐繞黃道軸作緩慢的進動,約26000年進動一周。這是產生歲差的原因。真地軸繞平地軸還有一種較快的周期運動。這種運動的周期大約為18.6年，根據《周髀算經》所說的”十九歲為一章”，天文學上稱這種運動為章動。章動可分為傾角章動和黃經章動。圖6概略地表示出地球的角運動。 上述研究結果在有重要實用意義的陀螺儀理論中得到廣泛的運用。高速自轉的陀螺儀在受到垂直於自轉軸分量的外力矩作用時，受迫運動就是瞬時回響的倒向外力矩方向的緩慢運動，這種運動稱為陀螺儀的進動。陀螺儀自轉軸的實際運動大都是在進動運動鄰近作極小幅度的快速抖動，這種抖動稱為陀螺儀的章動。如果引入一個假定：整個陀螺儀系統的動量矩可用陀螺儀轉子的自轉動量矩代替，則從動量矩定理出發就能導出陀螺儀的進動理論，由此算出的陀螺儀運動就只是進動。由於陀螺儀在飛行器和船艦的導航和穩定方面有重大使用價值，這方面的套用理論仍在深入研究之中。
參考書目
周培源編著：《理論力學》，人民教育出版社，北京，1952。
E.J.Routh,Dynamics of α System of Rigid Bodies,Dover, New York,1905.
R.N. Arneld and L. Maunder, Gyrodynamics & Its Engineering Application,Academic Press, New York,1961.
K. Magnus, de., Dynamics of Multibody Systems,Springer-Verlag, Berlin,Heidelberg,New York,1978.
