雅可比橢圓函式的定義
第一類橢圓積分
z=∫[(1-t^2)(1-k^2*t^2)]^(-1/2)dt (0~ω)
的反函式是雙周期的亞純函式,記作
ω=sn(z)=sn(z,k)
它具有基本周期:
ω=4K=4∫[1-k^2*sin(θ)^2]^(-1/2)dθ (0~π/2)
ω'=2iK'=2i∫[1-k’^2*sin(θ)^2]^(-1/2)dθ (0~π/2) k'=Sqr(1-k^2)
sn(z)稱為橢圓正弦,k為模,k‘為補模。若
sin(φ)=sn(z)
則稱φ為z的振幅函式,記作 φ=am(z) 又定義
cn(z)=cos(φ)=sqr(1-sn(z)^2) (橢圓餘弦)
tn(z)=tan(φ)=sn(z)/cn(z) (橢圓正切)
dn(z)=sqr(1-k^2*sn(z)^2)
上式中 sn(z) cn(z) tn(z) dn(z) 統稱雅可比橢圓函式,它們都是二階橢圓函式。
雅可比橢圓函式的性質
特殊點的值| z | 0 | K/2 | K | iK'/2 | K+iK'/2 | iK' | K+iK' |
| sn(z) | 0 | (1+k'^2)^(-1/2) | 1 | ik^(-1/2) | k^(-1/2) | ∞ | 1/k |
| cn(z) | 1 | sqr(k'/(1+k')) | 0 | sqr((k+1)/k) | -sqr((k-1)/k) | ∞ | -ik'/k |
| dn(z) | 1 | k'^(1/2) | k' | sqr(1+k) | sqr(1-k) | ∞ | 0 |
| 基本周期 | 零點 | 極點 | 留數 | |
| sn(z) | 4K 2iK' | 2mK+2niK' | 2mK+(2n+1)iK' | ((-1)^m)/k |
| cn(z) | 4K 2K+2iK' | (2m+1)K+2niK' | 2mK+(2n+1)iK' | ((-1)^(m+n))/(ik) |
| dn(z) | 2K 4iK' | (2m+1)K+(2n+1)iK' | 2mK+(2n+1)iK' | (-1)^(n-1)*i |
sn(mK+niK±z)
| ╲m n╲ | -1 | 0 | 1 | 2 | 2p |
| -1 | -dn(z)/(k*cn(z)) | ±1/(k*sn(z)) | dn(z)/(k*cn(z)) | 負正1/(k*sn(z)) | |
| 0 | -cn(z)/dn(z) | ±sn(z) | cn(z)/dn(z) | 負正sn(z) | |
| 1 | -dn(z)/(k*cn(z)) | ±1/(k*sn(z)) | dn(z)/(k*cn(z)) | 負正1/(k*sn(z)) | |
| 2 | -cn(z)/dn(z) | ±sn(z) | cn(z)/dn(z) | 負正sn(z) | |
| 2q | (-1)^p*sn(z) |
| ╲m n╲ | -1 | 0 | 1 | 2 | 2p |
| -1 | -(ik')/(kcn(z)) | ±(idn(z))/(ksn(z)) | (ik')/(kcn(z)) | 負正(idn(z))/(ksn(z)) | |
| 0 | ±(k'sn(z))/dn(z) | cn(z) | 負正(k'sn(z))/dn(z) | -cn(z) | |
| 1 | (ik')/(kcn(z)) | 負正(idn(z))/(ksn(z)) | -(ik')/(kcn(z)) | ±(idn(z))/(ksn(z)) | |
| 2 | 負正(k'sn(z))/dn(z) | -cn(z) | ±(k'sn(z))/dn(z) | cn(z) | |
| 2q | (-1)^(p+q)*cn(z) |
| ╲m n╲ | -1 | 0 | 1 | 2 | p |
| -1 | 負正(ik'sn(z))/cn(z) | ±(icn(z))/sn(z) | 負正(ik'sn(z))/cn(z) | ±(icn(z))/sn(z) | |
| 0 | k'/dn(z) | dn(z) | k'/dn(z) | dn(z) | |
| 1 | ±(ik'sn(z))/cn(z) | 負正(icn(z))/sn(z) | ±(ik'sn(z))/cn(z) | 負正(icn(z))/sn(z) | |
| 2 | -k'/dn(z) | -dn(z) | -k'/dn(z) | -dn(z) | |
| q | (-1)^q*dn(z) |
sn(z)^2+cn(z)^2=1
dn(z)^2+k^2*sn(z)^2=1
dn(z)^2-k^2*cn(z)^2=k'^2
am(-z)=-am(z)
sn(-z)=-sn(z)
cn(-z)=cn(z)
tn(-z)=-tn(z)
dn(-z)=-dn(z)
可見,雅可比橢圓函式的關係與圓函式(三角函式)相似。
轉換關係
加法公式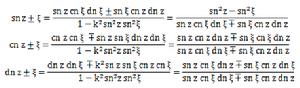 加法公式
加法公式-
-
-倍數公式
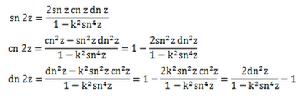 倍數公式
倍數公式-
-
-半數公式
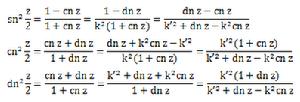 半數公式
半數公式-
-
-乘法公式
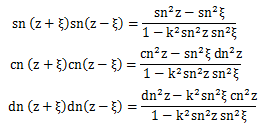 乘法公式
乘法公式-
-
-
-導數公式
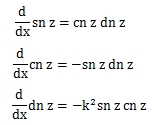 導數公式
導數公式-
-
-
-
-積分公式
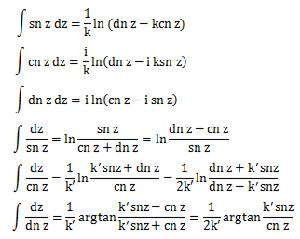 積分公式
積分公式