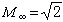定義
剛體繞一固定點的運動。繞固定點轉動的剛體只有一點不動，而其餘各點則分別在以該固定點為中心的同心球面上運動。支在固定球鉸鏈上的剛體、萬向聯軸節中的十字頭、萬向支架中的陀螺轉子等，都可以作這種運動。定點轉動的剛體通常用歐拉角ψ、θ、φ來定位。
剛體的定點轉動方程為：
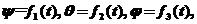剛體定點轉動式中t為時間。
達朗伯－歐拉定理
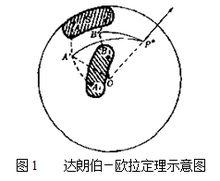
可表述為：定點轉動剛體的任何有限位移可用繞某軸的一次轉動來實現，該軸通過剛體的固定點。這個定理是J.le R.達朗伯於1749年,L.歐拉於1750年先後提出的，故得名。說明如下：
以中心在固定點O的任一球面截取剛體的截面圖形S（圖1）。在剛體的有限位移中，圖形內一點由A運動到A1，而另一點由B運動到B1，則大圓弧AA1的中垂面和大圓弧BB1的中垂面的交線OP*就是剛體這一有限位移的轉軸。
剛體定點轉動微小角位移
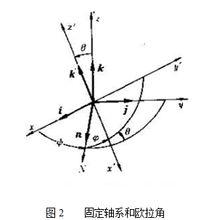
在短暫的時間間隔△t內，剛體繞軸OP*轉過一微小角度Θ，稱為角位移。它具有矢量的性質，可按平行四邊形規則相加。如用歐拉角定位，則當ψ、θ、φ有微小變化dψ、dθ、dφ時，剛體的微小角位移矢量Θ可表示成：
Θ=dψk+dθn+dφk′=Θi+Θj+Θk，
式中i、j、k為固定軸系Oxyz的單位矢；n、k′為節線和動基軸Oz′的單位矢（圖2）。
剛體定點轉動角速度
Δt趨向於零時，Θ趨於一個極限方向，Θ與Δt之比也趨於一個極限值ω。矢量ω稱為剛體在瞬時t的角速度，其數學表達式為：
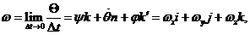剛體定點轉動式中
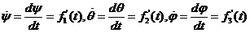剛體定點轉動分別是繞三個歐拉角的軸2、n、z′轉動的角速度。Δt→0時轉軸OP*所趨於的極限位置OP稱為剛體的瞬時軸，在每一瞬時，剛體以角速度ω繞瞬時軸轉動。
瞬軸錐面
隨著時間的推移，剛體的瞬時軸要改變位置，它在固定空間描出一個錐面，稱定瞬軸錐面（即空間極錐的錐面）；同時在剛體內部也描出一個錐面，稱為動瞬軸錐面（即本體極錐的錐面）。由此可得潘索定理：剛體定點轉動可用動瞬軸錐面在定瞬軸錐面上的純滾動來代替。
在定瞬軸錐面上，剛體的角速度矢ω的端點E描出的曲線稱為ω矢端圖（圖3）。
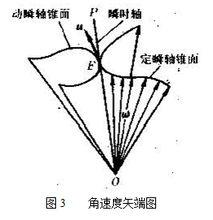剛體定點轉動角加速度
作定點轉動的剛體角速度 ω通常是變數。角速度變化 Δ ω與對應時間間隔Δ t的比值當Δ t→0時所趨至的極限值 ε稱為剛體在瞬時 t的角加速度，其數學表達式為：
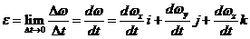剛體定點轉動可以把
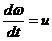剛體定點轉動視為 ω矢端 E沿矢端圖運動的速度。
里瓦斯公式
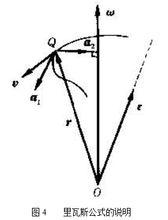
定點轉動剛體內任一點 Q的速度 v和加速度 a的公式，它們是：
v= ω× r， a= a1+ a2= ε× r+ ω× v，
式中 r為點 Q的矢徑; a1= ε× r為鏇轉加速度,沿著( ε， r)平面的法線，一般並不和速度 v共線； a2= ω× v為向軸加速度,恆垂直並指向瞬時軸(圖4)，但不是沿點 Q軌跡的主法線。
剛體定點轉動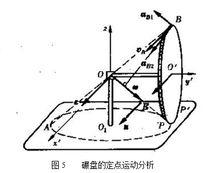
剛體定點轉動下面以分析碾盤的定點轉動為例作一說明。 如圖5所示，碾盤在固定水平面上繞固定點 O作無滑動的勻速滾動。碾盤和水平底盤相接觸之點 P┡的速度為零。 OP是瞬軸,定瞬軸錐面是圓錐 AOP,動瞬軸錐面是圓錐 P'OB。角速度矢 ω的端點 E具有線速度 u= ε，沿軸 Ox‘正向。碾盤上 B點的速度 v平行於軸 Ox’，加速度 a= a+ a且 a垂直於 OB和 Ox'所在平面，而 a垂直並指向瞬時軸 OP。
