非初等函式

非初等函式是指凡不是初等函式的函式。非初等函式的研究與發展是近現代數學的重大成就之一，極大拓展了數學在各個領域的套用，在機率論、物理學科各個分支中等有十分廣泛的套用。是函式的一個重要的分支。

注意

一般說來， 大部分分段函式不是初等函式。如符號函式，狄利克雷函式，gamma函式，誤差函式，Weierstrass函式。但是個別分段函式除外，例如右側的函式：

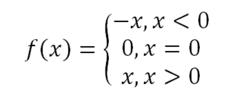非初等函式

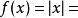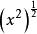非初等函式

非初等函式

由於此時 ，

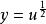非初等函式

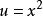非初等函式

是由函式 ， 複合而成的，所以該函式為初等函式。

然而同時取整函式（向下取整函式）：

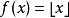非初等函式

非初等函式

卻不是初等函式。它的取值規定為距離 最近的整數，例如：

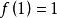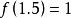非初等函式

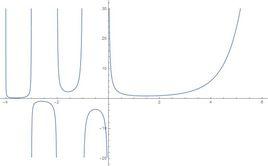
非初等函式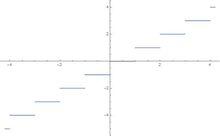

向下取整函式的圖像

於是又稱這樣的取整函式為“地板函式（Floor）”。它屬於符號函式的範疇。我們可以將其理解為是無窮多段的分段函式，所以說分段函式不一定是初等的，也不一定是非初等的。