分類方法
高等數學將基本初等函式歸為五類： 冪函式、指數函式、對數函式、三角函式、反三角函式 。
數學分析將基本初等函式歸為六類： 冪函式、指數函式、對數函式、三角函式、反三角函式、常數函式 。
下面一一介紹這些函式。
冪函式
定義
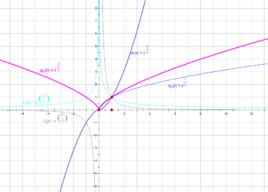
一般地，形如y=x (α為有理數）的函式，即以底數為自變數，冪為因變數，指數為常數的函式稱為 冪函式。例如函式y=x 、y=x 、y=x 、y=x （註：y=x =1/x y=x 時x≠0）等都是 冪函式。一般形式如下 ：
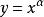基本初等函式（ α為常數，且可以是自然數、有理數，也可以是任意實數或複數。）
性質
冪函式的圖象一定會出現在第一象限內，一定不會出現在第四象限，至於是否出現在第二、三象限內，要看函式的奇偶性；冪函式的圖象最多只能同時出現在兩個象限內；如果冪函式圖象與坐標軸相交，則交點一定是原點。
冪函式取正值
當α>0時，冪函式y=x 有下列性質：
a、圖像都經過點（1,1）(0,0）；
b、函式的圖像在區間[0,+∞)上是增函式；
c、在第一象限內，α>1時，導數值逐漸增大；α=1時，導數為常數；0<α<1時，導數值逐漸減小，趨近於0；
冪函式取負值
當α<0時，冪函式y=x 有下列性質：
a、圖像都通過點（1,1）；
b、圖像在區間（0，+∞）上是減函式；（內容補充：若為X 易得到其為偶函式。利用對稱性，對稱軸是y軸，可得其圖像在區間（-∞，0）上單調遞增。其餘偶函式亦是如此）
c、在第一象限內，有兩條漸近線（即坐標軸），自變數趨近0，函式值趨近+∞，自變數趨近+∞，函式值趨近0。
冪函式取零
當α=0時，冪函式y=x 有下列性質：
y=x 的圖像是直線y=1去掉一點（0,1）。它的圖像不是直線 。
指數函式
定義
指數函式是數學中重要的函式。套用到值 e上的這個函式寫為exp( x)。還可以等價的寫為 e，這裡的 e是數學常數，就是自然對數的底數，近似等於 2.718281828，還稱為歐拉數。一般形式如下 ：
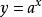基本初等函式（a>0, a≠1）
性質
當a>1時，指數函式對於 x的負數值非常平坦，對於 x的正數值迅速攀升，在 x等於0的時候，y等於1。當0<a<1時，指數函式對於 x的負數值迅速攀升，對於 x的正數值非常平坦，在 x等於0的時候，y等於1。在x處的切線的斜率等於此處y的值乘上lna。即由導數知識得：
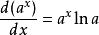基本初等函式
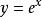基本初等函式作為實數變數 x的函式， 的圖像總是正的(在 x軸之上)並遞增(從左向右看)。它永不觸及 x軸，儘管它可以無限程度地靠近x軸(所以， x軸是這個圖像的水平漸近線。它的反函式是自然對數ln( x)，它定義在所有正數 x上。
指數函式
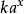基本初等函式有時，尤其是在科學中，術語 指數函式更一般性的用於形如 （k屬於R） 的函式，這裡的 a 叫做“底數”，是不等於 1 的任何正實數。本文最初集中於帶有底數為歐拉數e 的指數函式。
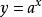基本初等函式指數函式的一般形式為 (a>0且≠1) (x∈R)，從上面我們關於冪函式的討論就可以知道，要想使得x能夠取整個實數集合為定義域，則只有使得a>0且a≠1。
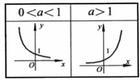
如圖所示為a的不同大小影響函式圖形的情況。
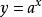基本初等函式在函式中可以看到 ：
（1） 指數函式的定義域為R，這裡的前提是a大於0且不等於1。對於a不大於0的情況，則必然使得函式的定義域不連續，因此我們不予考慮，同時a等於0函式無意義一般也不考慮。
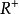基本初等函式（2） 指數函式的值域為 。
（3） 函式圖形都是上凹的。
（4） a>1時，則指數函式單調遞增；若0<a<1，則為單調遞減的。
指數函式（5） 可以看到一個顯然的規律，就是當a從0趨向於無窮大的過程中（不等於0）函式的曲線從分別接近於Y軸與X軸的正半軸的單調遞減函式的位置，趨向分別接近於Y軸的正半軸與X軸的負半軸的單調遞增函式的位置。其中水平直線y=1是從遞減到遞增的一個過渡位置。
（6） 函式總是在某一個方向上無限趨向於X軸,並且永不相交。
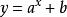基本初等函式（7） 函式總是通過（0，1）這點,(若 ,則函式定過點(0,1+b))
（8） 指數函式無界。
（9）指數函式是非奇非偶函式
（10）指數函式具有反函式，其反函式是對數函式，它是一個多值函式 。
對數函式
定義
一般地，函式y=logx（a>0，且a≠1）叫做對數函式，也就是說以冪（真數）為自變數，指數為因變數，底數為常量的函式，叫對數函式。
其中x是自變數，函式的定義域是（0，+∞），即x>0。它實際上就是指數函式的反函式，可表示為x=a 。因此指數函 數里對於a的規定，同樣適用於對數函式。一般形式如下 ：
基本初等函式（a>0, a≠1， x>0,特別當α=e時，記為y=ln x）
性質
定義域 求解：對數函式y=logx 的定義域是{x 丨x>0}，但如果遇到對數型複合函式的定義域的求解，除了要注意大於0以外，還應注意底數大於0且不等於1，如求函式y=log（2x-1）的定義域，需同時滿足x>0且x≠1和2x-1>0 ，得到x>1/2且x≠1，即其定義域為 {x 丨x>1/2且x≠1}。
值域 ：實數集R，顯然對數函式無界；
定點 ：對數函式的函式圖像恆過定點（1，0）；
單調性 ：a>1時，在定義域上為單調增函式；0<a<1時，在定義域上為單調減函式；
奇偶性 ：非奇非偶函式
周期性 ：不是周期函式
零點：x=1
注意： 負數和0沒有對數。
兩句經典話： 底真同對數正,底真異對數負。解釋如下：
也就是說：若y=logb （其中a>0,a≠1，b>0）
當0<a<1, 0<b<1時，y=logb>0;
當a>1, b>1時，y=logb>0;
當0<a<1, b>1時，y=logb<0;
當a>1, 0<b<1時，y=logb<0 。
三角函式
三角函式是數學中常見的一類關於角度的函式。也就是說以角度為自變數，角度對應任意兩邊的比值為因變數的函式叫三角函式，三角函式將直角三角形的內角和它的兩個邊長度的比值相關聯，也可以等價地用與單位圓有關的各種線段的長度來定義。三角函式在研究三角形和圓等幾何形狀的性質時有重要作用，也是研究周期性現象的基礎數學工具。在數學分析中，三角函式也被定義為無窮級限或特定微分方程的解，允許它們的取值擴展到任意實數值，甚至是複數值。
常見的三角函式包括正弦函式、餘弦函式和正切函式。在航海學、測繪學、工程學等其他學科中，還會用到如餘切函式、正割函式、餘割函式、正矢函式、半正矢函式等其他的三角函式。不同的三角函式之間的關係可以通過幾何直觀或者計算得出，稱為三角恆等式。
三角函式一般用於計算三角形中未知長度的邊和未知的角度，在導航、工程學以及物理學方面都有廣泛的用途。另外，以三角函式為模版，可以定義一類相似的函式，叫做雙曲函式。常見的雙曲函式也被稱為雙曲正弦函式、雙曲餘弦函式等等。三角函式（也叫做圓函式）是角的函式；它們在研究三角形和建模周期現象和許多其他套用中是很重要的。三角函式通常定義為包含這個角的直角三角形的兩個邊的比率，也可以等價的定義為單位圓上的各種線段的長度。更現代的定義把它們表達為無窮級數或特定微分方程的解，允許它們擴展到任意正數和負數值，甚至是複數值。
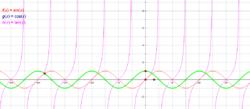
常見三角函式主要有以下 6 種：
正弦函式 ：y =sinx
三角函式圖像餘弦函式 ：y =cos x
正切函式 ：y =tan x
餘切函式 ：y =cot x
正割函式 ：y =sec x
餘割函式 ：y =csc x
此外，還有正矢、余矢等罕用的三角函式 。
反三角函式
反三角函式是一種基本初等函式。它是反正弦arcsin x，反餘弦arccos x，反正切arctan x，反餘切arccot x，反正割arcsec x,反餘割arccsc x這些函式的統稱，各自表示其反正弦、反餘弦、反正切、反餘切 ,反正割，反餘割為x的角。
它並不能狹義的理解為三角函式的反函式，是個多值函式。三角函式的反函式不是單值函式，因為它並不滿足一個自變數對應一個函式值的要求，其圖像與其原函式關於函式y=x對稱。歐拉提出反三角函式的概念，並且首先使用了“arc+函式名”的形式表示反三角函式。
主要有以下 6 個 ：
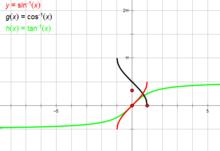使用幾何畫板繪製的三角函式圖像反正弦函式：y = arcsin x
反餘弦函式：y = arccos x
反正切函式：y = arctan x
反餘切函式：y = arccot x
反正割函式：y = arcsec x
反餘割函式：y = arccsc x
常數函式
定義
在數學中， 常數函式（也稱常值函式）是指值不發生改變（即是常數）的函式。例如，我們有函式 f(x)=4，因為 f映射任意的值到4，因此 f是一個常數。更一般地，對一個函式 f: A→B，如果對 A內所有的 x和 y，都有 f(x)=f(y)，那么， f是一個常數函式。
請注意，每一個空函式（定義域為空集的函式）無意義地滿足上述定義，因為 A中沒有 x和 y使 f(x)和 f(y)不同。然而有些人認為，如果包括空函式的話，那么常數函式將更容易定義。
對於多項式函式，一個非零常數函式稱為一個零次多項式。下列為一般形式 ：
y=C (C是常數)
性質
常數函式可以通過與複合函式的關係，從兩個途徑進行描述。
下面這些是等價的：
f: A→B是一個常數函式。 對所有函式 g, h: C→A, fog=foh（“o”表示複合函式）。 f與其他任何函式的複合仍是一個常數函式。 上面所給的常數函式的第一個描述，是範疇論中常數態射更多一般概念的激發和定義的性質。
根據定義，一個函式的導函式度量自變數的變化與函式變化的關係。那么我們可以得到，由於常數函式的值是不變的，它的導函式是零。例如：
如果 f是一個定義在某一區間、變數為實數的實數函式，那么若且唯若 f的導函式恆為零時， f是常數。 對預序集合間的函式，常數函式是保序和倒序的；相反的，如果 f既是保序的也是倒序的，如 f的定義域是一個格，那么 f一定是一個常數函式。
常數函式的其他性質包括：
任一定義域和陪域相同的常數函式是等冪的。 任一拓撲空間上的常數是連續的。 在一個連通集合中，若且唯若 f是常數時，它是局部常數 。
