函式周期性
函式周期性的關鍵的幾個字“有規律地重複出現”。
當自變數增大任意實數時(自變數有意義),函式值有規律的重複出現。
假如函式f(x)=f(x+T)(或f(x+a)=f(x-b)其中a+b=T),則說T是函式的一個周期.T的整數倍也是函式的一個周期。
說明
1.概念的提出:將日曆中“星期”隨日期變化的周期性的出現和正弦函式值隨角的變化周期性的出現進行對比,尋求出兩者實質:當“自變數”增大某一個值時,“函式值”有規律的重複出現。
出示函式周期性的定義:對於函式y=f(x),假如存在一個非零常數T,使得當x取定義域內的任何值時,f(x+T)=f(x)都成立,那么就把函式y=f(x)叫做周期函式,不為零的常數T叫做這個函式的周期。
“當自變數增大某一個值時,函式值有規律的重複出現”這句話用數學語言的表達.
2.定義:對於函式y=f(x),如果存在一個不為零的常數T,使得當x取定義域內的每一個值時,f(x+T)=f(x)
概念的具體化:
當定義中的f(x)=sinx或cosx時,思考T的取值。
T=2kπ(k∈Z且k≠0)
所以正弦函式和餘弦函式均為周期函式,且周期為 T=2kπ(k∈Z且k≠0)
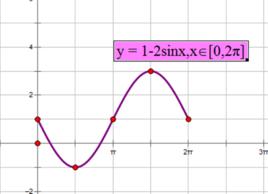
展示正、餘弦函式的圖象。
周期函式的圖象的形狀隨x的變化周期性的變化。(用課件加以說明。)
強調定義中的“當x取定義域內的每一個值”
令(x+T)2=x2,則x2+2xT+T2=x2
所以2xT+T2=0, 即T(2x+T)=0
所以T=0或T=-2x
強調定義中的“非零”和“常數”。
例:三角函式sin(x+T)=sinx
cos(x+T)=cosx中的T取2π
3. 最小正周期的概念:
對於一個函式f(x),如果它所有的周期中存在一個最小的正數,那么這個最小正數叫f(x)的最小正周期。
對於正弦函式y=sinx, 自變數x只要並且至少增加到x+2π時,函式值才能重複取得。所以正弦函式和餘弦函式的最小正周期是2π。(說明:如果以後無特殊說明,周期指的就是最小正周期。)
在函式圖象上,最小正周期是函式圖象重複出現需要的最短距離。
4.例:求下列函式的周期:
(1)y=3cosx
分析:cosx中的自變數只要且至少增加到x+2π時,函式cosx的值才重複出現,因而函式3cosx的值也才重複出現,因此y=3cosx的周期是2π.(說明cosx前面的係數和周期無關。)
(2)y=sin(x+π/4)
分析略,說明在x後面的角也不影響周期。
(3)y=sin2x
分析:因為sin2(x+π)=sin(2x+2π)=sin2x, 所以自變數x只要且至少增加到x+π時,函式值就重複出現。所以原函式的周期為π。(說明x的係數對函式的周期有影響。)
(4) y=cos(x/2+π/4) (分析略)
(5)y=sin(ωx+φ) (分析略)
結論:形如y=Asin(ωx+φ) 或y=Acos(ωx+φ) (A,ω,φ為常數,A0, xR) 的函式的周期為T=2π/ω
周期函式性質:
(1)若T(≠0)是f(X)的周期,則-T也是f(X)的周期。
(2)若T(≠0)是f(X)的周期,則nT(n為任意非零整數)也是f(X)的周期。
(3)若T1與T2都是f(X)的周期,則T1±T2也是f(X)的周期。
(4)若f(X)有最小正周期T*,那么f(X)的任何正周期T一定是T*的正整數倍。
 函式周期性
函式周期性(5)T*是f(X)的最小正周期,且T1、T2分別是f(X)的兩個周期,則 (T1+T2)\T*Q(Q是有理數集)
(6)若T1、T2是f(X)的兩個周期,且 是無理數,則f(X)不存在最小正周期。
(7)周期函式f(X)的定義域M必定是雙方無界的集合。
其他周期函式
1.常函式為周期函式,但無最小正周期,其周期為任意實數。
2.Dirchlet函式
D(X)=
{1 X為有理數時
{0 X為無理數時
復指數函式:y=e^(jwt),其中j為虛數單位,w為任意實數,t為自變數。
重要推論
如果函式f(x)(x∈D)在定義域內有兩條對稱軸x=a,x=b則函式f(x)是周期函式,且周期T=2|b-a|(不一定為最小正周期)。
如果函式f(x)(x∈D)在定義域內有兩個對稱中心A(a,0),B(b,0)則函式f(x)是周期函式,且周期T=2|b-a|(不一定為最小正周期)。
如果函式f(x)(x∈D)在定義域內有一條對稱軸x=a和一個對稱中心B(b, 0)(a≠b),則函式f(x)是周期函式,且周期T=4|b-a|(不一定為最小正周期)。
1.如果函式f(x)(x
2.如果函式f(x)(x
3.如果函式f(x)(x