算法實例
函式f(x)±g(x)最小正周期的求法
定義法
概念：根據周期函式和最小正周期的定義，確定所給函式的最小正周期。
例1、求函式y=|sinx|+|cosx|的最小正周期.
解:∵ =|sinx|+|cosx|
=|－sinx|+|cosx|
=|cos(x+π/2)|+|sin(x+π/2)|
=|sin(x+π/2)|+|cos(x+π/2)|
=f(x+π/2)
對定義域內的每一個x，當x增加到x+π/2時，函式值重複出現，因此函式的最小正周期是π/2.（如果f（x+T）=f（x），那么T叫做f（x）的周期）。
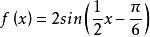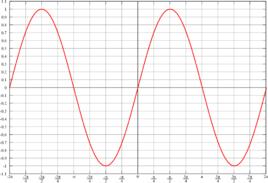
最小正周期例2 、求函式的最小正周期。
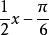最小正周期解：把看成是一個新的變數z,那么2sinz的最小正周期是2π。
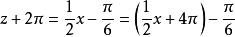最小正周期由於。所以當自變數x增加到x+4π且必須增加到x+4π時，函式值重複出現。
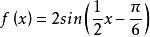最小正周期∴函式的最小正周期是4π。
公式法
這類題目是通過三角函式的恆等變形，轉化為一個角的一種函式的形式，用公式去求，其中正餘弦函式求最小正周期的公式為T=2π/|ω| ，正餘切函式T=π/|ω|。
函式f(x)=Asin(ωx+φ)和f(x)=Acos(ωx+φ)(A≠0,ω>0）的最小正周期都是；函式f(x)=Atan(ωx+φ)和f(x)=Acot(ωx+φ)(A≠0,ω>0）的最小正周期都是，運用這一結論，可以直接求得形如y=Af(ωx+φ)(A≠0,ω>0）一類三角函式的最小正周期（這裡“f”表示正弦、餘弦、正切或餘切函式）。
例3、求函式y=cotx－tanx的最小正周期.
解：y=1/tanx－tanx=(1－tan^2· x)/tanx=2*(1－tan^2·x)/(2tanx)=2cot2x
∴T=π/2
函式為兩個三角函式相加，若角頻率之比為有理數，則函式有最小正周期。
最低公倍數法
設f(x)與g(x)是定義在公共集合上的兩個三角周期函式，T1、T2分別是它們的周期，且T1≠T2，則f(x)±g(x)的最小正周期T1、T2的最低公倍數，分數的最低公倍數=T1,T2分子的最低公倍數/T1、T2分母的最大公約數。
求幾個正弦、餘弦和正切函式的最小正周期，可以先求出各個三角函式的最小正周期，然後再求期最低公倍數T,即為和函式的最小正周期 。
例4、求函式y=sin3x+cos5x的最小正周期.
解：設sin3x、cos5x的最小正周期分別為T1、T2，則T1=2π/3,T2=2π/5 ，所以y=sin3x+cos5x的最小正周期T=2π/1=2π.
例5、求y=sin3x+tan2x/5 的最小正周期.
解：∵sin3x與tan2x/5 的最小正周期是2π/3與5π/2,其最低公倍數是10π/1=10π.
∴y=sin3x+tan2x/5的最小正周期是10π.
說明：幾個分數的最低公倍數，我們約定為各分數的分子的最低公倍數為分子，各分母的最大公約數為分母的分數。
圖象法
概念：作出函式的圖象，從圖象上直觀地得出所求的最小正周期。
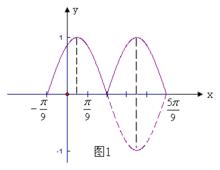
例6、求y=|sinx|的最小正周期.
解：由y=|sinx|的圖象
可知y=|sinx|的周期T=π.
最小正周期例7、求下函式的最小正周期。
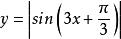最小正周期（1）
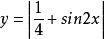最小正周期（2）
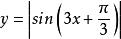最小正周期解：（1）先作出函式的圖象（見圖1）
觀察圖象，易得所求的周期為T=π/3。
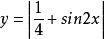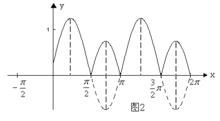
最小正周期 最小正周期（2）先作出的圖象（見圖2）
觀察圖象，易得所求的周期為T=π。
恆等變換法
概念：通過對所給函式式進行恆等變換，使其轉化為簡單的情形，再運用定義法、公式法或圖象法等求出其最小正周期 。
(1) f(x)=sin(x+π/3)cos(x-π/3)
(2) f(x)=sin x+cos x
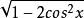最小正周期(3) f(x)=
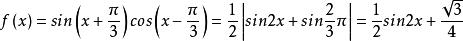最小正周期解 (1)
∴最小正周期為T= π
(2) f(x)=sin x+cos x
=(sin x+cos x)(sin x-sin xcos x+cos x)
=(sin x-sin xcos x+cos x)
=(sin x+cos x)2-3sin xcos x
=1-3/4sin x
=5/8+3/8cos4x
∴最小正周期為T=π/2
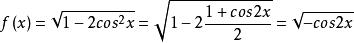最小正周期(3)
它與－cos2x的周期相同，故得 f(x)的最小正周期為T=π
補充問題
函式f(x)=sin2x-4sin³xcosx(x∈R)的最小正周期為（ B ）
A.π/4 B.π/2 C.π D.2π
