數學分析中, 偽微分運算元是微分運算元的推廣。偽微分運算元在偏微分方程和量子場論等領域有廣泛的套用。
歷史
偽微分運算元的研究始於20世紀60年代中期,Kohn,Nirenberg,Hörmander,Unterberger和Bokobza[1]的工作。
他們在Atiyah-Singer指數定理的第一個證明中發揮了重要作用。Atiyah和Singer感謝Hörmander幫助理解偽微分運算元的理論 。
動機
常係數線性微分運算元
 偽微分運算元
偽微分運算元 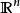 偽微分運算元
偽微分運算元 設 為一個定義在 上的緊支撐的光滑函式,考慮下面的常數係數微分運算元:
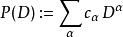 偽微分運算元
偽微分運算元 利用傅立葉變換,可以將這個微分運算元用另外一種等價的形式表達,首先將這個運算元的傅立葉變換寫出,
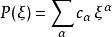 偽微分運算元
偽微分運算元 注意這裡已經將微分變換為頻率域中的乘法,所以整個運算元的傅立葉變換成為一個頻率域中的多項式。我們一般稱其為一個 符號( symbol)。
這個符號的傅立葉逆變換為
 偽微分運算元
偽微分運算元 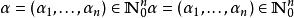 偽微分運算元
偽微分運算元 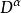 偽微分運算元
偽微分運算元 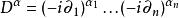 偽微分運算元
偽微分運算元 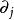 偽微分運算元
偽微分運算元 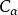 偽微分運算元
偽微分運算元  偽微分運算元
偽微分運算元 注意,上面的 表示了一個多重指標,而 則是利用這個多重指標定義的一個微分運算元,具體可以寫為 ,其中 表示對第j個變數的微分。另外,各個係數 都是 中的常數。
從(1)中不難發現,一個微分運算元可以用它的傅立葉變換表示出來。類似地,一個 偽微分運算元也可以這樣定義:
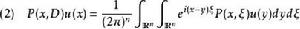 偽微分運算元
偽微分運算元 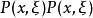 偽微分運算元
偽微分運算元 與(1)的區別在於,這裡的 可以是一個更一般的函式。
式( 1 )是如何得到的
如上選取的u,其傅立葉變換為
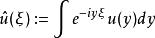 偽微分運算元
偽微分運算元 而從傅立葉逆變換公式可以知道
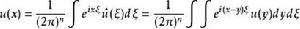 偽微分運算元
偽微分運算元 將P(D)套用於這個u,則有
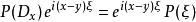 偽微分運算元
偽微分運算元 由此就得到了(1)。
利用偽微分運算元表示偏微分方程的解
為了求解方程
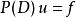 偽微分運算元
偽微分運算元 我們可以形式地將傅立葉變換套用於方程兩邊,從而得到一個 代數的方程
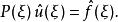 偽微分運算元
偽微分運算元 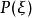 偽微分運算元
偽微分運算元 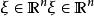 偽微分運算元
偽微分運算元 如果符號對於任何都不是0,那么除以後則有
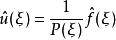 偽微分運算元
偽微分運算元 由傅立葉逆變換公式,則可以得到一個解
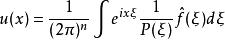 偽微分運算元
偽微分運算元 請注意我們的假設:
1.P(D)是一個 常係數的微分運算元。
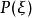 偽微分運算元
偽微分運算元 2.它的符號 永遠不為0。
3.u和f都有傅立葉變換。
最後一個條件可以利用和分布相關的定理減弱(這裡的分布不是統計中的分布,而是分析中的概念),而前面兩個條件則可以利用如下的方法減弱:
將f的傅立葉變換寫出可以得到
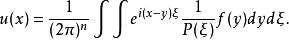 偽微分運算元
偽微分運算元 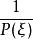 偽微分運算元
偽微分運算元 此式的形式與(1)非常相似,區別僅在不是一個多項式函式,而是一個更一般的函式,因此引出下面的主題:
符號類和偽微分運算元
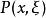 偽微分運算元
偽微分運算元 我們核心的目的是通過公式(1),在允許使用更一般的 的條件下,定義運算元P(x,D):
 偽微分運算元
偽微分運算元 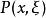 偽微分運算元
偽微分運算元 因此假設屬於某個特定的 符號類。
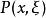 偽微分運算元
偽微分運算元 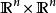 偽微分運算元
偽微分運算元 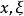 偽微分運算元
偽微分運算元 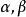 偽微分運算元
偽微分運算元 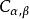 偽微分運算元
偽微分運算元 例如,如果 是 一個上無限可微的函式,並且對於所有 和所有多重指標 ,以及某些給定的常數 ,給定的實數m,P都滿足
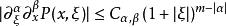 偽微分運算元
偽微分運算元 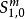 偽微分運算元
偽微分運算元 那么P就屬於一個Hörmander類,我們將它記為
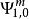 偽微分運算元
偽微分運算元 而對應的運算元P(x,D)則被稱為一個 m 階的偽微分運算元,並且屬於類 。
性質
一個係數為有界光滑函式的m階線性微分運算元是一個m階的偽微分運算元。
兩個偽微分運算元P,Q的複合PQ也是一個偽微分運算元,而且PQ的符號可以用P和Q的符號來計算。
一個偽微分運算元的伴隨運算元和轉置運算元仍然是一個偽微分運算元。
如果一個m階微分運算元是一個(m階一致的)橢圓運算元並且可逆,那么它的可逆運算元是一個-m階的偽微分運算元,並且可以算出它的符號。這就意味著在某種意義下,人們可以利用偽微分運算元的理論,精確地求解線性橢圓微分方程。
一個微分運算元是 局部的,因為它只需要知道被作用的函式在某個點附近的某個鄰域中的值,就可以求出這個運算元在這個點附近作用的效果。而偽微分運算元有時也被非正式地被叫做 偽局部的,因為它作用在一個分布上的時候,不會在這個分布的光滑部分產生新的奇點。
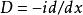 偽微分運算元
偽微分運算元 如同一個微分運算元可以用 的記號,以P(x,D)表出(其中P是D的多項式,稱為 符號),偽微分運算元的符號可以用比多項式更一般的函式表示。一般而言,人們可以將一個偽微分運算元的分析問題轉化為一個與它的符號相關的一系列代數問題,而這也是微局部分析的基本思想。
偽微分運算元的核
偽微分運算元可以用核來表示。核在對角線上的奇異性取決於相應運算元的程度。實際上,如果符號滿足上述微分不等式且m≤0,就可以證明該核是一個奇異積分核。
相關概念
• 微分代數和微分環上定義偽微分運算元的微分代數
• 傅立葉變換
• 傅立葉積分運算元
• 振盪積分運算元
• Sato's基本定理
