運算元描述
在邊緣檢測中，常用的一種模板是Sobel 運算元。Sobel 運算元有兩個，一個是檢測水平邊緣的 ；另一個是檢測垂直邊緣的 。與Prewitt運算元相比，Sobel運算元對於象素的位置的影響做了加權，可以降低邊緣模糊程度，因此效果更好。
Sobel運算元另一種形式是各向同性Sobel(Isotropic Sobel)運算元，也有兩個，一個是檢測水平邊緣的 ，另一個是檢測垂直邊緣的 。各向同性Sobel運算元和普通Sobel運算元相比，它的位置加權係數更為準確，在檢測不同方向的邊沿時梯度的幅度一致。將Sobel運算元矩陣中的所有2改為根號2，就能得到各向同性Sobel的矩陣。
由於Sobel運算元是濾波運算元的形式，用於提取邊緣，可以利用快速卷積函式， 簡單有效，因此套用廣泛。美中不足的是，Sobel運算元並沒有將圖像的主體與背景嚴格地區分開來，換言之就是Sobel運算元沒有基於圖像灰度進行處理，由於Sobel運算元沒有嚴格地模擬人的視覺生理特徵，所以提取的圖像輪廓有時並不能令人滿意。 在觀測一幅圖像的時候，我們往往首先注意的是圖像與背景不同的部分，正是這個部分將主體突出顯示，基於該理論，我們給出了下面閾值化輪廓提取算法，該算法已在數學上證明當像素點滿足常態分配時所求解是最優的。
計算方法
索貝爾運算元邊緣運算元所採用的算法是先進行加權平均，然後進行微分運算，運算元的計算方法如下：
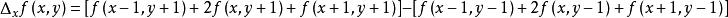索貝爾運算元
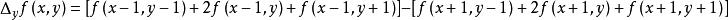索貝爾運算元
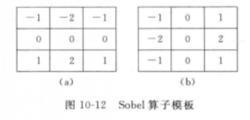索貝爾運算元Sobel運算元垂直方向和水平方向的模板如圖10-12所示，前者可以檢測出圖像中的水平方向的邊緣，後者則可以檢測圖像中垂直方向的邊緣。實際套用中，每個像素點取兩個模板卷積的最大值作為該像素點的輸出值，運算結果是一副邊緣圖像。
核心公式
該運算元包含兩組3x3的矩陣，分別為橫向及縱向，將之與圖像作平面卷積，即可分別得出橫向及縱向的亮度差分近似值。如果以A代表原始圖像，Gx及Gy分別代表經橫向及縱向邊緣檢測的圖像，其公式如下:
索貝爾運算元圖像的每一個像素的橫向及縱向梯度近似值可用以下的公式結合，來計算梯度的大小。
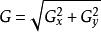索貝爾運算元然後可用以下公式計算梯度方向。
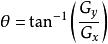索貝爾運算元在以上例子中，如果以上的角度θ等於零，即代表圖像該處擁有縱向邊緣，左方較右方暗。
細化邊緣
在對圖象的研究和套用中,人們往往僅對圖象中的某些部分感興趣,這些部分通常稱為目標或前景,其餘部分則稱為背景. 將圖象分為目標和背景的操作稱為圖象分割.圖象分割是由圖象處理進到圖象分析的關鍵步驟. 多年來,圖象分割一直得到人們的高度重視,至今已提出了上千種分割算法. 它們大致可分為閾值法、邊緣檢測法和區域生長法等幾大類 .在這些方法中,人們對閾值法較為重視,現在還不時有新的方法提出來.而對於後兩種方法則注意較少,已有的方法基本上還是60～ 70年代提出的. 究其原因,是由於閾值法方法比較簡單, 且計算量也較少些.但其缺點是,除了自適應閾值法外,其閾值的選取主要是根據灰度分布的直方圖,而很少考慮象素的空間關係.當圖象比較複雜時,目標與背景就不能簡單地用一個閾值來分離. 這時就只有求助於邊緣檢測法或區域生長法. 而邊緣檢測法中最為常用的是Sobel運算元.
Sobel運算元的優點是方法簡單、處理速度快,並且所得的邊緣光滑、連續.其缺點是邊緣較粗,由於處理時需作兩值化處理,故得到的邊緣與閾值的選取也有很大的關係.本文提出的邊緣細化方法是通過引入衰減因子而得到不失真的灰階邊緣圖,再用Sobel運算元進行細化,對於邊緣較陡的部分可以得到光滑、連續,且接近單點寬的邊緣;而對於邊緣模糊的部分,這種過程可以重複多次,也可得到較細的邊緣(但不一定連續) .同時,這種方法還可保留低幅值的邊緣.這樣,既可提高定位精度,又可得到用其它方法難以得到的模糊邊緣和微弱邊緣. 而且對用其它邊緣檢測方法得到的邊緣進行處理,此方法也有效.
邊緣細化的套用大致可有以下幾種情況:
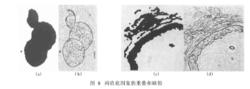索貝爾運算元( 1) 重疊對象的分離,如圖8(a )兩值圖象上的3個細胞無法分割,而從細化的邊緣圖(圖8( b ) )中可得到分割所需的邊緣信息.
( 2) 缺損對象的補齊,如圖8( c)兩值圖象上的血管管壁,其內側有缺損,而從細化的邊緣圖中(圖8( d) )可得到補齊的所需邊緣信息.
( 3) 可補上閾值選取不當而遺漏的對象,如圖8細胞和血管壁的邊緣圖上都多出了一個小顆粒.
( 4) 由於邊緣以灰度差為分離參數,且邊緣線較細,故定位較準確,檢測效果比閾值法要好,這有利於測量精度的提高.
本方法的缺點是處理效果與邊緣本身的質量有關,若邊緣質量好,且分界線較陡,則效果較好,反之則較差,而且還不適用於理想階躍輸入. 這些可從圖中看出. 另外,細化邊緣圖可能“信息過量” ,從中直接提取邊緣也很困難,最好能與其它特徵,如原灰階圖、閾值圖等一起考慮,可作為它們的補充. 如用閾值方法尋找對象,再用此方法精確定位.
套用實例
使用MATLAB進行Sobel運算元的可視化邊緣檢測，程式如下圖所示：
索貝爾運算元其顯示結果如圖17-6所示。
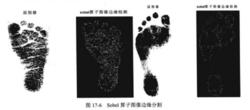索貝爾運算元採用Sobel對腳印圖像的邊緣檢測可知，採用Sobel運算元對圖像進行邊緣檢測，紋理檢測效果一般，邊緣檢測斷斷續續，不具後續處理。Sobel運算元是一階離散性差分運算元， 用來運算圖像亮度函式的梯度之近似值。Sobel運算元並沒有將圖像的主體與背景嚴格地區 分開來.即Sobel運算元沒有基於圖像灰度進行處理，由於Sobel運算元沒有嚴格地模擬人的 視覺生理特徵，所以提取的圖像輪廓有時並不能令人滿意。
