拉普拉斯運算元
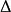四維導數運算元
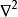四維導數運算元
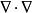四維導數運算元在數學以及物理中， 拉普拉斯運算元或是 拉普拉斯算符（英語： Laplace operator, Laplacian）是由歐幾里得空間中的一個函式的梯度的散度給出的微分運算元，通常寫成、 或。
這名字是為了紀念法國數學家皮埃爾-西蒙·拉普拉斯（1749–1827）而命名的。他在研究天體力學在數學中首次套用運算元，當它被施加到一個給定的重力位（Gravitational potential）的時候，其中所述運算元給出的質量密度的常數倍。經拉普拉斯運算元運算為零∆f=0的函式稱為調和函式，現在稱為拉普拉斯方程，和代表了在自由空間中的可能的重力場。
拉普拉斯運算元有許多用途，此外也是橢圓運算元中的一個重要例子。
拉普拉斯運算元出現描述許多物理現象的微分方程里。例如，常用於波方程的數學模型、熱傳導方程、流體力學以及亥姆霍茲方程。在靜電學中，拉普拉斯方程和泊松方程的套用隨處可見。在量子力學中，其代表薛丁格方程式中的動能項。
拉普拉斯運算元是最簡單的橢圓運算元，並且拉普拉斯運算元是霍奇理論的核心，並且是德拉姆上同調的結果。在圖像處理和計算機視覺中，拉普拉斯運算元已經被用於諸如斑點檢測和邊緣檢測等的各種任務。
定義
四維導數運算元
四維導數運算元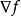
四維導數運算元 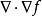四維導數運算元 四維導數運算元拉普拉斯運算元是 n維歐幾里得空間中的一個二階微分運算元，其定義為對函式先作梯度運算（）後，再作散度運算（）的結果。因此如果是二階可微的實函式，則的拉普拉斯運算元定義為：
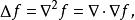四維導數運算元 四維導數運算元
四維導數運算元的拉普拉斯運算元也是笛卡兒坐標系中的所有非混合二階偏導數：
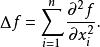四維導數運算元作為一個二階微分運算元，對於 k≥ 2，拉普拉斯運算元把 C函式映射到 C函式。表達式定義了一個運算元Δ： C( R)→ C( R)，或更一般地，定義了一個運算元Δ： C(Ω)→ C(Ω)，對於任何開集Ω。
函式的拉普拉斯運算元也是該函式的海森矩陣的跡：
四維導數運算元坐標表示式
二維空間
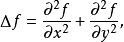四維導數運算元其中 x與 y代表x-y平面上的笛卡兒坐標
另外極坐標的表示法為：
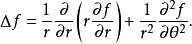四維導數運算元三維空間
笛卡兒坐標系下的表示法
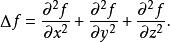四維導數運算元圓柱坐標系下的表示法
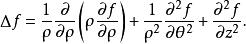四維導數運算元球坐標系下的表示法
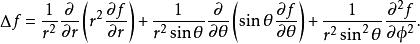四維導數運算元N維空間
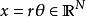四維導數運算元
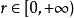四維導數運算元
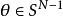四維導數運算元在參數方程為（其中以及）的N 維球坐標系中，拉普拉斯運算元為：
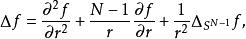四維導數運算元
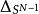四維導數運算元
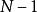四維導數運算元
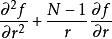四維導數運算元
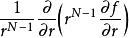四維導數運算元其中是維球面上的拉普拉斯-貝爾特拉米運算元。我們也可以把的項寫成。
推廣
複雜空間上的實值函式
拉普拉斯運算元可以用一定的方法推廣到非歐幾里得空間，這時它就有可能是橢圓型運算元，雙曲型運算元，或超雙曲型運算元。
在閔可夫斯基空間中，拉普拉斯運算元變為達朗貝爾運算元：
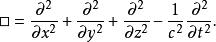四維導數運算元達朗貝爾運算元通常用來表達克萊因-戈爾登方程以及四維波動方程。第四個項前面的符號是負號，而在歐幾里德空間中則是正號。因子 c是需要的，這是因為時間和空間通常用不同的單位來衡量；如果 x方向用寸來衡量， y方向用厘米來衡量，也需要一個類似的因子。
值域為複雜空間
向量值函式的拉普拉斯運算元
拉普拉斯運算元作用在向量值函式上，其結果被定義為一個向量，這個向量的各個分量分別為向量值函式各個分量的拉普拉斯，即
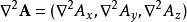四維導數運算元更一般地，對沒有坐標的向量，我們用下面的方式定義（受向量恆等式的啟發）：
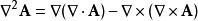四維導數運算元，也可用類似於拉普拉斯－德拉姆運算元的方式定義，然後證明“旋度的旋度”向量恆等式．
拉普拉斯－貝爾特拉米運算元
主條目：拉普拉斯－貝爾特拉米運算元和拉普拉斯－德拉姆運算元
拉普拉斯運算元也可以推廣為定義在黎曼流形上的橢圓型運算元，稱為 拉普拉斯-貝爾特拉米運算元。達朗貝爾運算元則推廣為偽黎曼流形上的雙曲型運算元。拉普拉斯–貝爾特拉米運算元還可以推廣為運行於張量場上的運算元（也稱為拉普拉斯–貝爾特拉米運算元）。
另外一種把拉普拉斯運算元推廣到偽黎曼流形的方法，是通過 拉普拉斯–德拉姆運算元，它作用在微分形式上。這便可以通過外森比克恆等式來與拉普拉斯–貝爾特拉米運算元聯繫起來。
