定義
就像拉普拉斯運算元一樣，定義拉普拉斯－貝爾特拉米運算元為梯度的散度。為了寫出這個運算元的一個公式，首先需寫出流形上的散度與梯度。
設g表示流形上的（偽）-度量張量，我們發現在局部坐標中體積形式由
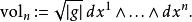拉普拉斯-貝爾特拉米運算元
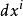拉普拉斯-貝爾特拉米運算元給出，這裡 是局部坐標系基向量
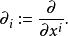拉普拉斯-貝爾特拉米運算元
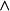拉普拉斯-貝爾特拉米運算元
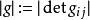拉普拉斯-貝爾特拉米運算元的對偶基1-形式，而 是楔積。這裡 是度量張量行列式的絕對值。流形上一個向量場 X的散度可以定義為
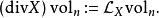拉普拉斯-貝爾特拉米運算元
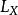拉普拉斯-貝爾特拉米運算元這裡 是沿著向量場 X的李導數。在局部坐標中，我們得到
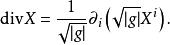拉普拉斯-貝爾特拉米運算元
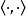拉普拉斯-貝爾特拉米運算元這裡（下面同樣如此）使用了愛因斯坦求和約定，所以上式其實是一個關於 i的和式。一個數量函式 f的梯度利用流形上內積可定義為
拉普拉斯-貝爾特拉米運算元
拉普拉斯-貝爾特拉米運算元 拉普拉斯-貝爾特拉米運算元對位於流形在 x點的切空間中所有向量 成立。這裡 df是函式 f的外導數；它是變數 的一個函式。在局部坐標中有
拉普拉斯-貝爾特拉米運算元綜上，對一個數量函式 f的拉普拉斯–貝爾特拉米運算元在局部坐標中公式為
拉普拉斯-貝爾特拉米運算元
拉普拉斯-貝爾特拉米運算元
拉普拉斯-貝爾特拉米運算元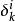
拉普拉斯-貝爾特拉米運算元這裡 是度量張量 g之逆的分量，所以 ，這裡 為克羅內克函式。
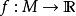拉普拉斯-貝爾特拉米運算元注意到如上定義中，只對數量函式 有效。我們欲將對函式的拉普拉斯運算元，延拓到微分形式上；為此，我們必須回到拉普拉斯–德拉姆運算元，將在下一節定義。可以證明拉普拉斯–貝爾特拉米運算元在歐幾里得空間退化通常的拉普拉斯運算元，利用乘積法則與鏈式法則將其重寫為
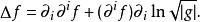拉普拉斯-貝爾特拉米運算元當|g|=1，比如笛卡兒坐標下的歐幾里得空間，容易得到
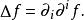拉普拉斯-貝爾特拉米運算元
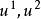拉普拉斯-貝爾特拉米運算元這就是通常的拉普拉斯運算元。利用符號為 (+++-) 的閔可夫斯基度量，得到達朗貝爾運算元。在局部參數化 中，拉普拉斯–貝爾特拉米運算元利用度量張量與克里斯托費爾符號可表示如下：
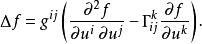拉普拉斯-貝爾特拉米運算元注意到通過使用球坐標與圓柱坐標的度量張量，我們類似地可重新得到拉普拉斯運算元在球坐標與圓柱坐標下的表達式。拉普拉斯–貝爾特拉米運算元不僅在彎曲空間中存在，而且在曲線坐標系下的通常平坦空間中也存在。
另外注意到外導數 d與 -div伴隨：
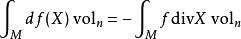拉普拉斯-貝爾特拉米運算元（證明）
這裡最後一個等式利用了斯托克斯定理。另外注意拉普拉斯–貝爾特拉米運算元是負的且對稱：
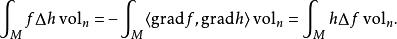拉普拉斯-貝爾特拉米運算元對函式 f與 h。因此，許多作者定義拉普拉斯–貝爾特拉米運算元時添一個減號，將其變成正的。
利用共變導數
拉普拉斯–貝爾特拉米運算元也可利用與列維-奇維塔聯絡相伴的疊代共變導數的跡寫出來。從這個觀點來看，設 X是切向量場的一個基（不必由坐標系誘導）。則一個函式 f的黑塞矩陣是一個 2-張量，分量由
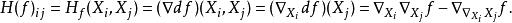拉普拉斯-貝爾特拉米運算元給出。容易看出有張量性變換，因為對每個變數 X與 X都是線性的。則拉普拉斯–貝爾特拉米運算元是黑塞矩陣關於度量的跡：
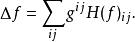拉普拉斯-貝爾特拉米運算元在抽象指標記號中，此運算元經常寫成
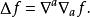拉普拉斯-貝爾特拉米運算元需要理解清楚的是這個跡其實就是黑塞張量的跡。
拉普拉斯－德拉姆運算元
定義
更一般地，我們可以在微分流形的外代數上定義一個拉普拉斯微分運算元。在黎曼流形上它是一個橢圓型運算元，而在洛倫茲流形上是雙曲型的。拉普拉斯–德拉姆運算元定義為
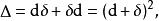拉普拉斯-貝爾特拉米運算元
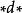拉普拉斯-貝爾特拉米運算元這裡 d 是外導數而 δ 是余微分。當作用在數量函式上，余微分可以定義為 δ = −，這裡* 是霍奇星運算元；更一般地，余微分可能包含與所作用的 k-形式的階數有關的一個符號。
可以證明拉普拉斯–德拉姆運算元作用在數量函式 f上時與前面的拉普拉斯–貝爾特拉米運算元定義相同；細節參見證明。注意拉普拉斯–德拉姆運算元事實上是負拉普拉斯–貝爾特拉米運算元；這個符號來自定義余微分的習慣。不幸的是，兩者都用 Δ 表示，經常成為混亂之源。
性質
給定數量函式 f與 h，以及一個實數 a，拉普拉斯–德拉姆運算元有如下性質：
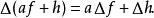拉普拉斯-貝爾特拉米運算元
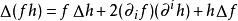拉普拉斯-貝爾特拉米運算元（證明）
張量上的拉普拉斯運算元
利用與列維-奇維塔聯絡相伴的共變導數，拉普拉斯–貝爾特拉米運算元可推廣到偽黎曼流形上任意張量。這個推廣的運算元可以作用在反對稱張量上。但所得的運算元與拉普拉斯–德拉姆運算元給出的不同：兩者通過外森比克恆等式相關。
例子
拉普拉斯–貝爾特拉米運算元許多特例可以明白地寫出來。
•球面拉普拉斯運算元
球面拉普拉斯運算元是帶截面曲率為 1 的典範度量 n-1 維球面上的拉普拉斯–貝爾特拉米運算元。通常將其視為等距嵌入 R中，作為以原點為中心的單位球面。則對 S上一個函式 f，其球面拉普拉斯運算元定義為
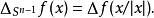拉普拉斯-貝爾特拉米運算元這裡 f( x/| x|) 是函式 f次數為零的齊次延拓到 R，而 Δ 是周圍歐幾里得空間的拉普拉斯運算元。具體地，這由歐幾里得拉普拉斯運算元在球極坐標下熟知的公式所蘊含：
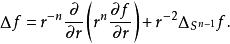拉普拉斯-貝爾特拉米運算元更一般地，利用法叢可進行類似的技巧，定義任何黎曼流形作為等距嵌入歐幾里得空間中的超平面上的拉普拉斯–貝爾特拉米運算元。
我們也可以給出球面上拉普拉斯–貝爾特拉米運算元在法坐標系中一個內蘊描述。設 ( t, ξ) 是球面上關於球面上特定點 p（北極）的球坐標，這就是關於 p的測地極坐標。這裡 t表示從 p出發沿著單位速度測地線的緯度， ξ是表示 S中測地線的方向的一個參數。則球面拉普拉斯運算元具有如下形式
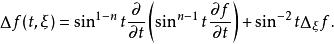拉普拉斯-貝爾特拉米運算元
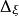拉普拉斯-貝爾特拉米運算元這裡是通常 n- 1 球面上的拉普拉斯運算元。
相關條目
•微分幾何中的拉普拉斯運算元（Laplacian operators in differential geometry）
