波動方程簡介
波動方程歷史上許多科學家，如達朗貝爾、歐拉、丹尼爾·伯努利和拉格朗日等在研究樂器等物體中的弦振動問題時，都對波動方程理論作出過重要貢獻。
弦振動方程是在18世紀由達朗貝爾（d'Alembert）等人首先系統研究的，它是一大類偏微分方程的典型代表。
方程形式
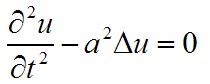波動方程對於一個標量quantity u的波動方程的一般形式是：
{ \partial^2 u \over \partial t^2 } = c^2 \nabla^2u
這裡c通常是一個固定常數，也就是波的傳播速率(對於空氣中的聲波大約是330米/秒, 參看音速)。對於弦的振動，這可以有很大的變化範圍：在上（slinky），它可以慢到1米/秒。但若c作為波長的函式改變，它應該用相速度代替：
v_\mathrm = \frac{\omega}.
注意波可能疊加到另外的運動上（例如聲波的傳播在氣流之類的移動媒介中）。那種情況下，標量u會包含一個(對於沿著流運動的波為正，對於反射波為負)。
u = u(x,t), 是振幅,在特定位置x和特定時間t的波強度的一個測量。對於空氣中的聲波就是局部氣壓，對於振動弦就使從靜止位置的位移。\nabla^2 是相對於位置變數x的拉普拉斯運算元。注意u可能是一個標量或向量。
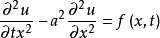如，一維波動方程：
波動方程二維波動方程：
波動方程三維波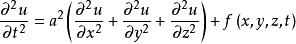動方程：
波動方程方程的解及條件
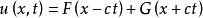波動方程對於一維標量波動方程的一般解是由達朗貝爾給出的：
, 其中
和
為任意兩個可微分的單變數函式，分別對應於右傳播波，和左傳播波。要決定
和
必須考慮兩個初始條件：
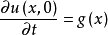波動方程
波動方程這樣達朗貝爾公式變成了：
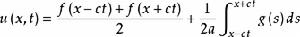波動方程在經典的意義下，如果f(x) \in C^k並且g(x) \in C^則u(t,x) \in C^k.
一維情況的波動方程可以用如下方法推導：想像一個質量為m的小質點的佇列，互相用長度h的彈簧連線。彈簧的硬度為k :
這裡u (x)測量位於x的質點偏離平衡位置的距離。對於位於x+h的質點的運動方程是：
m{\partial^2u(x+h,t) \over \partial t^2}= kLINK
其中u(x)的時間依賴性變成顯式的了。
要點分析
如果在所考慮的區域內自由電荷的體密度為零（ρ=0），且媒質是均勻、線性、各向同性的，則由這些條件下的麥克斯韋方程組及本構關係可以導得
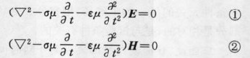波動方程稱為廣義波動方程或基爾霍夫方程。式中的稱為拉普拉斯算符。在直角坐標系中
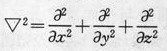波動方程在自由空間或絕緣良好的介質中，電導率可以忽略不計，即σ=0，於是E和H的微分方程成為
波動方程稱為波動方程或達朗貝爾方程。
波動方程的解是在空間中一個沿特定方向傳播的電磁波。對於電磁波傳播問題的分析，都可歸結為在給定的邊界條件和初始條件下求波動方程的解。
標量波動方程 套用直角坐標系
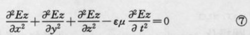波動方程
波動方程可以把③寫成
即把矢量波動方程分解成三個標量波動方程，每個方程中只含一個知函式。但只有在套用直角坐標系時才能得到這樣的結果，在其它坐標系中，通過分解而得的三個標量方程都具有複雜的形式。
亥姆霍茲方程 在場源按正弦規律隨時間變化的條件下，場量也是同頻率的正弦函式，可以用相量表示。由相量形式的麥克斯韋方程組出發，可以推導出相量形式的波動方程：
波動方程式中：
波動方程式⑧與⑨又稱亥霍茲方程。
