阿佩爾方程

阿佩爾方程是一個與物理學相關的小作品。在經典力學中，阿佩爾方程適用於非完整系的動力學方程，是在1900年由阿佩爾描述。

阿佩爾方程

正文

法國數學家 P.-┵.阿佩爾導出的適用於非完整系統的重要動力學方程，其形式為：

　(1)

式中G為吉布斯函式，它是加速度動能式用準加速度囧（s =1,2,...,N ）表示之式；為對應於準坐標πs的廣義力;N是系統的自由度。由於完整系統是非完整系統的特例，因此，凡是適用於非完整系統的動力學方程，亦適用於完整系統。
假定一個有n個質點的非完整系統，它含l個有限約束

和r個微分約束

　(2)

可先利用有限約束，將3n個x用 m＝3n-l個廣義坐標q1，q2，...，qm表示，r個微分約束用qi和妜i(i=1,2,...,m)表示。由此可變換式（2）為：

，　(3)

式中m個妜j（j=1,2,...,m）只有N(=m-r)個是獨立的。為了更一般化,採用m個妜的線性式組成N個準速度囜來描述這系統，即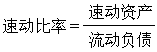

。

由於非完整系統的微分約束（3）是不可積的,所以坐標πs不一定存在,這就是πs是準坐標名稱的由來。囜的時間導數囧稱為準加速度。 由於式（1）左邊是對囧的偏導數，所以G中一切不含囧的項都可以捨去不寫,從而使計算G函式的工作量大為減少。
圓球、圓輪在粗糙面上無滑動地滾動，溜冰鞋在冰上的滑行等都是非完整系統力學問題的例子。
參考書目
　W.D.MacMillan,Dynamics of Rigid Bodies,McGraw-Hill,New York,1936.
　E.T.Whittaker,A Treatise on the Analytical Dynamicsof　Particles and　Rigid Bodies,4th ed.,Cambridge Univ.Press,Cambridge,1952.
　汪家訸編:《分析力學》,高等教育出版社,北京,1983。

配圖

相關連線