KdV方程

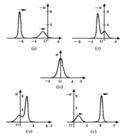KdV方程是1895年由荷蘭數學家科特韋格(Korteweg)和德弗里斯(de Vries)在研究淺水中小振幅長波運動時共同發現的一種單向運動淺水波偏微分方程（也有人稱之為科特韋格-德弗里斯方程，但一般都習慣直接叫KdV方程）。

y't+6y*y'x+y'''x=0()

KdV方程的解為簇集的孤立子（又稱孤子，孤波）。

KdV方程

KdV方程和物理問題有幾個聯繫。 它是弦在Fermi-Pasta-Ulam問題在連續極限下的統治方程。KdV方程也描述弱非線性回復力的淺水波。

KdV方程也可以用逆散射技術求解，譬如那些適用於薛丁格方程的。