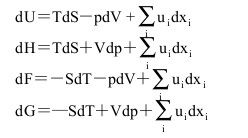正文
對於一個多組分均相系統,偏摩爾熱力學函式XB定義為: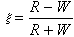 (1)
(1)
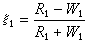 表示在系統的溫度T、壓力p及除物質B外其他組分的物質的量nC都不改變的條件下,系統的某一廣延量X隨物質B的物質的量變化的變化率。
表示在系統的溫度T、壓力p及除物質B外其他組分的物質的量nC都不改變的條件下,系統的某一廣延量X隨物質B的物質的量變化的變化率。 多組分均相系統的任一廣延量均有其相應的偏摩爾熱力學函式,例如
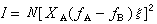 稱為物質B的偏摩爾體積;
稱為物質B的偏摩爾體積;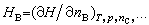 稱為物質B的偏摩爾焓;
稱為物質B的偏摩爾焓;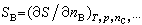 稱為物質B的偏摩爾熵。
稱為物質B的偏摩爾熵。 系統的偏摩爾熱力學函式是強度量,其數值取決於系統的溫度、壓力和組成,而與系統內物質的總量無關。
在多組分均相系統中,系統內任一廣延量的數值取決於系統的溫度、壓力及系統中各組分的物質的量,因此廣延量X的全微分表達式可寫為:
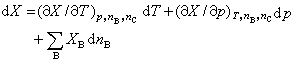 (2)
(2)
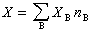 (3)
(3)
式(3)稱為偏摩爾熱力學函式的集合公式。此式表明,系統的某一廣延量的數值等於系統中各物質的物質的量與其相應的偏摩爾熱力學函式的乘積之和。
將式(3)取全微分並與式(2)相比較,可得:
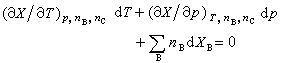 (4)
(4)
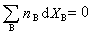 (5)
(5)
在偏摩爾熱力學函式中,偏摩爾吉布斯函式是最有用的,它又稱為化學勢,用符號μB表示,其定義為:
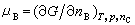 (6)
(6)
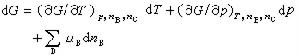 (7)
(7)
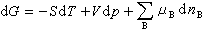 (8)
(8)
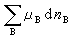 項代表當系統中的某些物質的物質的量發生變化時所引起系統吉布斯函式的變化。
項代表當系統中的某些物質的物質的量發生變化時所引起系統吉布斯函式的變化。 如果系統經歷一個等溫等壓變化,則式(8)成為:
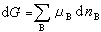 (9)
(9)
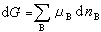 <0時,該變化過程為自發過程,當
<0時,該變化過程為自發過程,當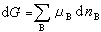 =0時,該變化過程為可逆過程,即系統處於平衡狀態。
=0時,該變化過程為可逆過程,即系統處於平衡狀態。 將上述結論用於相變過程和化學反應過程,可以得到以下推論:
① 在一個多相系統中,物質總要從化學勢高的相自動地向化學勢低的相轉移。當系統中的每一種物質在各相中的化學勢相等時(即
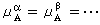 ,
,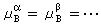 ,
,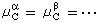 ,式中角標A、B、C、…為不同的物質;α、β、…為不同的相),系統達到相平衡。
,式中角標A、B、C、…為不同的物質;α、β、…為不同的相),系統達到相平衡。 ② 若一個多組分系統中的化學反應符合下述條件:
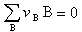 (10)
(10)
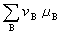 <0時,反應能自動地正向進行。系統達到化學平衡時,則符合:
<0時,反應能自動地正向進行。系統達到化學平衡時,則符合: 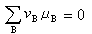 (11)
(11)
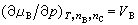 (12)
(12)
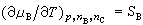 (13)
(13)
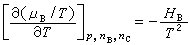 (14)
(14)