定義
方程式:
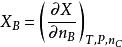 偏摩爾量
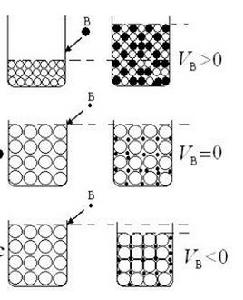
偏摩爾量對於純物質,並不存在偏摩爾量的概念,它就是摩爾量。
偏摩爾體積可以看作是某一定濃度溶液中1摩爾該組分對體系總體積的貢獻。
在理解偏摩爾量時。要注意以下幾點:
(1)只有均相系統的廣度性質才有偏摩爾量。偏摩爾量本身是強度性質,它與系統的溫度、壓強及各組分的組成有關,而與系統內物質的總量無關。
(2)偏微分的條件必須是恆溫、恆壓。
(3)對於純物質的均相系統,顯然偏摩爾量即為該物質的摩爾量。
分析
我們知道,不論是什麼體系,物質的質量(克)和物質的量(摩爾)總是具有加和性的。但是,體系的其他廣度性質則不一定具有簡單的加和性。以體積這一廣度性質為例,兩組分混合前的體積之和(V+V)與混合後的實際體積(V)並不相等,即V+V≠V。要找出規律,須引入“偏摩爾量”這個新概念。
在多組分(k個組分)的均相混合體系中,某一廣度性質Z(例如V、U、H、G),是T和P和各物質物質的量n的函式,即
Z=f(T,P,n,n,……n),顯然,Z的全微分為若體系發生的過程為等溫等壓過程,dT=0,dP=0,則Z=f(n,n)
式中n是除B物質以外的所有其他物質物質的量,B不同,n也要相應變化。現令
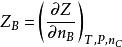 偏摩爾量
偏摩爾量稱為B物質的某廣度性質Z的偏摩爾量。
從定義式可以看出,偏摩爾量的物理意義是:在等溫等壓下,往無限大的體系中加入1摩爾B物質而引起體系廣度性質Z的改變數;或者是,在有限的體系中加入微量B物質dn而引起Z的微小變化dZ之比。
例如,若V表示水的偏摩爾體積,則其物理意義是在恆溫等壓下,往無限大的體系(此體系不一定是由水組成)中加入1mol水,體系體積的變化量;或往有限的體系中加入微量的水(之所以限制微量,是為了保證體系n不變)而引起該體系體積的變化。G表示體系中氯化鈉的偏摩爾吉布斯自由能,物理意義是往體系中加入微量氯化鈉而引起該體系吉布斯自由能的變化量。
問題
1、只有廣度性質才有對應的偏摩爾量。因為只有廣度性質才與體系中物質的量有關。偏摩爾量也是狀態函式,是強度性質。
2、只有均相多組分體系才使用偏摩爾量的概念。單組分體系的偏摩爾量等於其摩爾量。
3、對於均相多組分體系,也只有恆溫等壓,n不變的條件下,體系的廣度性質Z對n的偏微商才是偏摩爾量。
4、熱力學關係式中的廣度性質(U、H、G等),用該廣度性質的偏摩爾量來代替也成立。
性質
多組分體系的所有熱力學關係均可寫成以偏摩爾量表示的對應關係,即將單組分系統的摩爾量換成多組分系統的偏摩爾量即可,熱力學函式關係並不發生變化。引入偏摩爾量。為多組分體系熱力學函式的研究帶來了很大的方便;系統的容量性質等於各組分偏摩爾量與其物質的量的乘積之和。如(A+B)二元溶液的體積V=nV+nV加和性給出了體系的總量與各組分的偏摩爾量的關係。