研究歷史
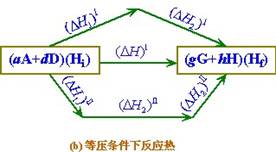反應熱示意圖熱力學第一定律給出了熱和功相互轉化的數量關係。為了提高熱機效率，1824年卡諾提出了著名的卡諾定理，他得到的結論是正確的，但他卻引用了錯誤的“熱質論”。為了進一步闡明卡諾定理，1850年克勞修斯提出熱力學第二定律，他認為：“不可能把熱從低溫物體傳到高溫物體而不引起其他變化”，相當於熱傳導過程的不可逆性。
1851年開爾文認為：“不可能從單一熱源取熱使之完全變為有用的功而不引起其他變化”，相當於摩擦生熱過程的不可逆性。除上述兩種說法外，熱力學第二定律還有幾種不同的敘述方式，它們之間是等效的。在研究化學反應時，需要確定熵的參考態。
1912年，能斯脫提出熱力學第三定律，即絕對溫度的零點是不可能達到的。其他科學家還提出過幾種不同表述方式，其中1911年普朗克的提法較為明確，即“與任何等溫可逆過程相聯繫的熵變，隨著溫度的趨近於零而趨近於零”。這個定律非常重要，為化學平衡提供了根本性原理。
吉布斯給出了熱力學原理的更為完美的表述形式，用幾個熱力學函式來描述系統的狀態，使化學變化和物理變化的描述更為方便和實用。他發表了著名的“相律”，對相平衡的研究起著重要的指導作用。但實際系統常常是開放的、非平衡的，所涉及的物理化學過程通常是不可逆的。
19世紀人們開始研究熱導擴散和電導等現象，但僅僅限於對近似平衡的非平衡狀態和過程的研究。20世紀60年代，開始對遠離平衡的非平衡狀態和過程的研究以後，熱力學理論取得了重大的進展。昂薩格和普里戈金等都曾作出傑出的貢獻。
研究內容
相關書籍熱化學
主要內容是用熱力學第一定律研究“化學反應熱”方面的問題。在化學反應中，一摩爾物質的變化（指主要的生成物或反應物）所吸收的熱量名為化學反應熱，簡稱為反應熱。根據熱力學第一定律知道，在定溫、定壓（或定容）下發生的化學反應，其反應熱Qp（或Qp）等於反應過程焓（或內能）的變化 ΔH(或ΔU)。所以方程 
(1)是熱化學中的基本熱力學公式。利用態函式U、H 的性質，就可以從某些已知的反應熱計算未知的反應熱。由式(1)可見，反應熱Qp(或Qp)僅由反應物的初始狀態及生成物的終了狀態所決定，而與中間過程無關，這稱為赫斯 (Hess)定律。例如化學反應 C O2─→CO2可以分
和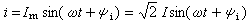
兩步實現，若這三個反應的反應熱分別為Qp、Qp1、Qp2，則 Qp＝Qp1 Qp2。赫斯定律是熱力學第一定律的早期實驗基礎之一，它可以幫助人們從易於測定的Qp(或Qp)值，計算難於測定的Qp（或Qp）值；它是熱化學中的重要定律之一。
反應熱與溫度的關係由基爾霍夫定律給出。它的內容是：定壓下，在兩個不同溫度(T1和T2)進行的同一化學反應，其反應熱Qp(T1)和Qp(T2)不同。由赫斯定律可導出反應熱隨溫度的變化滿足如下關係 
(2)式中ΔCp為生成物的定壓熱容和反應物的定壓熱容之差。式(2)就是基爾霍夫定律，它也是熱化學中的一個重要定律。
化學平衡
主要內容是套用熱力學的平衡判據研究化學反應的平衡條件。在化學熱力學中通常把化學反應方程寫作等式，例如，在化學熱力學中將高溫下氫分子和氧分子化合成水的反應式寫為2H2O－2H2－O2=0。一般地，把任意一個化學反應寫作如下形式
(3)
式中Ai表示第i種組元。vi表示第i種組元在化學反應中的計量係數，並規定對生成物而言vi取正號，對反應物vi取負號。
對在不同條件下發生的化學反應，可使用不同的平衡判據。例如，在恆溫、恆壓、恆組成(N)下進行的化學反應，其自發進行（相應於下式中的小於號）或平衡條件（相應於下式的等號）由自由焓判據確定。即
(4)式中μi為系統中某物種的偏摩爾自由焓（或稱化學勢），dni為該物種摩爾數的變化。
由於化學反應 vAA vBB …─→vLL vM M … (5) 發生時，各物種的數量變化dni要服從計量係數之間的比例關係，即
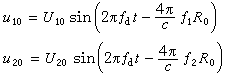(6)
dGT，p，N=(-vAμA-vBμB vLμL vMμM)dξ≤0 (7) 或
(8)
為在恆溫、恆壓、恆組成的系統中單位進度的反應（按計量係數的摩爾數發生的反應）產生的自由焓變值 Δ埥。為了滿足恆組成的條件，可以構想系統非常大，因而發生了單位進度的化學反應後，系統的組成只變了無窮小量。Δ埥稱為反應自由焓，-Δ埥稱為化學親合勢。Δ埥越小（或－Δ埥 越大）則在該T、E、N(組成)時，反應趨勢越大；Δ埥 等於零時，反應達到平衡。
當系統中沒有產物時，產物的化學勢為零;這時Δ埥＝
即正向反應趨勢極大；反之，若反應物的濃度為零，則Δ埥＝∞，即逆向反應趨勢極大。在反應的過程中，組成不斷變化，Δ埥值也隨之變化，變化的情況如附圖中所示，正向反應的Δ埥由AB曲線表示，逆向反應的Δ埥由A┡B┡曲線表示。R為反應物，P為產物。O點處Δ埥＝0，所以O代表平衡混合物。
化學熱力學
(9)μi為平衡系統中第i個組元的化學勢。當系統為理想氣體時，μi＝μ孂(T) RT lnpi。μ孂(T)為一個與溫度有關的常數，稱為標準化學勢，Ei為平衡系統中第i個組元的分壓，R 為摩爾氣體常數。聯合平衡條件式(9)，可以得到平衡系統中各組元分壓Ei之間的關係 
(10)
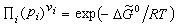。 (11)
稱為標準反應自由焓。由式 (11)知道，
在恆溫下為一常數，稱為平衡常數， 以Kp表示 Kp＝ (12)
的關係得到 
， (13)
， (14)
Ka，Kx是平衡常數的另兩種表示方法。
當系統處於非平衡態時，設其組元的分壓為E媴，則當
時，反應正向進行；當 
時，反應逆向進行。
溶液理論
用熱力學方法研究多組元體系的理論。 溶液是液態溶體。溶體是一個含有兩種或兩種以上組元的均勻系。當溶體是氣相時，通常叫做混合氣體;當溶體是固相時，叫做固溶體。
在研究溶液性質方面，理想溶液是一個十分重要的模型。化學勢具有以下形式
(15)
的溶液稱為理想溶液。式中xi表示組元 i在溶液中的摩爾分數；
是溫度T與壓強E的函式。形成理想溶液的各組元在T、E不變的情形下混合時，總體積不變，也不吸收或放出熱量，但其熵的變化為
。實際溶液的性質與理想溶液的有差別，但非常稀的溶液，或化學結構極為相似的組元混合而成的溶液，均很接近理想溶液，例如苯和甲苯形成的溶液。此外將理想溶液服從的規律經過“校正”，就可以研究非理想溶液的性質。
理想溶液的蒸氣壓與組元濃度的關係服從喇烏耳定律。設溶液與其蒸氣達到平衡，並把蒸氣看作混合理想氣體，其中第i組元的化學勢為 
(16)μ孂是在溫度T及1個大氣壓時第i組元純氣體的化學勢。若在同溫度時，此純液體的蒸氣壓是E孂，則按照喇烏耳定律，有
(17)式中xi為第i組元在液相中的摩爾分數。將式(17)代入式(16)可得
。 (18)由於在平衡系統中μi=μig，所以對比式(15)及式(18)得出
(19)在理想溶液中，任一組元從xi＝0到xi＝1都服從式(15)，即無論是溶劑還是溶質，在整個濃度範圍內都服從喇烏耳定律。
常遇到的溶液是稀溶液，即其中一種組元的數量遠遠大於其他組元的數量。數量占得較少的溶質不服從喇烏耳定律而服從亨利定律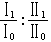 
(20)因而對於溶質在式(15)中的 
(21) 除上述溶液的蒸氣壓受到溶質摩爾分數(或說濃度)的影響外，隨著溶質濃度的增加，溶液的沸點升高而凝固點下降，這些性質在實際中均有重要套用。
非理想體系中各組元的化學勢與壓力(或摩爾分數)之間的關係比較複雜，但將理想體系中各組元的化學勢的表達式加以“校正”，就可使其既適用於理想體系又適用於非理想體系，在形式上統一起來。為了達到這一目的，G.N.路易斯提出了逸度f與活度α的概念。在真實氣體混合物中，用逸度fi代替理想混合氣體中的分壓Ei，則化學勢表達為 μi=μ孂＋RTlnfi。 (22)逸度f相當於“校正壓力”，它與T、E及混合物的組成有關。與此相似，在溶液中用活度αi，代替第i組元的摩爾分數，則化學勢表達為 μi=μ孂＋RTlnai。(23)活度αi是第i組元的化學勢的量度，它與T、E及溶液的組成有關，相當於“校正濃度”。逸度與壓力的比值稱為逸度係數；活度與摩爾分數的比值稱為活度係數。二者代表非理想體系與理想體系偏差大小的量度，可以通過實驗方法測定。
基本定律
相關書籍化學熱力學的核心理論有三個：所有的物質都具有能量，能量是守恆的，各種能量可以相互轉化；事物總是自發地趨向於平衡態；處於平衡態的物質系統可用幾個可觀測量描述。
化學熱力學是建立在三個基本定律基礎上發展起來的。熱力學第一定律就是能量守恆和轉化定律，它是許多科學家實驗總結出來的。一般公認，邁爾於1842年首先提出普遍“力”(即現在所謂的能量)的轉化和守恆的概念。焦耳1840～1860年間用各種不同的機械生熱法，進行熱功當量測定，給能量守恆和轉化概念以堅實的實驗基礎，從而使熱力學第一定律得到科學界的公認。
熱力學三個基本定律是無數經驗的總結，尚未發現熱力學理論與事實不符合的情形，因此它們具有高度的可靠性。熱力學理論對一切物質系統都適用，具有普遍性的優點。這些理論是根據巨觀現象得出的，因此稱為巨觀理論，也叫唯象理論。
熱力學所根據的基本規律就是熱力學第一定律、第二定律和第三定律，從這些定律出發，用數學方法加以演繹推論，就可得到描寫物質體系平衡的熱力學函式及函式間的相互關係，再結合必要的熱化學數據，解決化學變化、物理變化的方向和限度，這就是化學熱力學的基本內容和方法。
經典熱力學是巨觀理論，它不依賴於物質的微觀結構。分子結構理論的發展和變化，都無需修改熱力學概念和理論，因此不能只從經典熱力學獲得分子層次的任何信息。並且它只處理平衡問題而不涉及這種平衡狀態是怎樣達到的，只需要知道系統的起始狀態和終止狀態就可得到可靠的結果，不涉及變化的細節，所以不能解決過程的速率問題。欲解決上述兩個局限性問題，需要其其它學科如化學統計力學、化學動力學等的幫助。
熱力學理論已經解決了物質的平衡性質問題，但是關於非平衡現象，現有的理論還是初步的，有待進一步研究；熱力學在具體問題中的實際套用，仍有廣闊的發展前途。
