合金熱力學
合金熱力學的理論基礎 經典熱力學 經典熱力學是現象理論。它所依據的是從無數經驗歸納出的三個定律,然後從此演繹出許多描述物質平衡性質的關係式。熱力學第一定律是力學中機械能轉換和守恆定律的延伸。若環境對體系作功W,體系又從環境吸熱Q,則體系的內能增加ΔU為:
ΔU=W+Q (1)
或 dU=δW +δQ (1a)
由於U是狀態函式,才能寫為全微分;而W 及Q隨過程而有所不同,不能寫為全微分。
熱力學第二定律指出了過程方向,它的一種表達方式便是熵增原理:
dS(總)=(dS(體)+dS(環))≥0 (2)
式中dS(體)、dS(環)及dS(總)分別表示體系、環境和總熵的全微分;(2)式中“=” 表示平衡關係;“>” 表示過程方向。熵的概念是在19世紀研究熱機效率時提出的:從狀態 1到狀態 2的熱量變化是隨途徑而異的,而可逆過程的
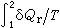 則與途徑無關。人們定義熵S的全微分為:
則與途徑無關。人們定義熵S的全微分為: dS呏δQr/T (3)
δQr是可逆過程的熱量變化,T是絕對溫度,由於S是狀態函式,故可寫為全微分。
熱力學第三定律是為了計算熵的絕對值的。凝聚系的熵在恆溫過程中改變值ΔS 隨絕對溫度降低而趨於零。即:
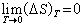 (4)
(4)
 (5)
(5)
熱力學第一及第二定律分別引入體系的狀態函式U及S,為了分析問題的方便,定義了焓H、自由能F及自由焓G
H呏U+pV (6)
F呏U-TS (7)
G呏H-TS (8)
式中p及V分別是體系的壓強和體積。合併第一及第二定律,可以獲得關閉體系(與環境沒有物質交換)的平衡條件(=)及過程方向(<)為:
(dU)v,S≤0 (9)
(dH)p,S≤0 (10)
(dF)v,T≤0 (11)
(dG)p,T≤0 (12)
由於p、V、T、S、U、H、F、G都是狀態函式,藉助於微分方程,可以導出許多表述物質平衡現象的關係式。例如,考慮可逆過程的膨脹功(pdV),則合併第一定律(1)式及第二定律(3)式得到:
dU=TdS-pdV (13)
利用上式及H、F、G定義,可以分別得到:
dH=TdS+Vdp (14)
dF=-SdT-pdV (15)
dG=-SdT+Vdp (16)
若再考慮可逆過程的其他功(下表),
 合金熱力學
合金熱力學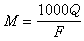 (17)
(17)
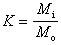 (18)
(18)
 合金熱力學
合金熱力學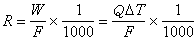 (19)
(19)
由於在液態和固態金屬的研究中,p和V常變化較小,可以忽略不計,所以G和F的判據常可互換使用。
經典熱力學是熱學的一部分,而熱學的特有實驗技術是測溫(T)及量熱(Q)。從(6)及(11)式得到:
ΔH=Q+W+pΔV+VΔp
若體系只作可逆膨脹功(-pΔV),則在恆壓(Δp=0)下的熱效應Qp便是ΔH:
ΔH=Qp (20)
恆壓下熱容Cp,即使體系升高1℃所需的熱為:
 (21)
(21)
Cp易於測定,一般具備如下形式:
Cp=a+bT-cT-2 (23)
式中a、b及c是隨體系而異的係數。合併上列二式便可從實驗上確定ΔH;而套用第二定律(3)式及實驗測定的δQr,便可獲得ΔS;再利用F及G的定義【(7)、(8)式】,便可獲得ΔF 及ΔG。
化學熱力學 化學熱力學研究體系化學變化過程的熱力學問題。套用經典熱力學處理化學問題時,需要兩個新的概念:成分和相。一般用摩爾數ni或摩爾分數xi來表示組元的成分:
 (24)
(24)
 (25)
(25)
 (26)
(26)
 nj表示除i組元外,其他組元都不變的情況。在k元系中兩相(A+B)平衡時,每一個組元在 A 及 B 相中的化學勢必須相等:
nj表示除i組元外,其他組元都不變的情況。在k元系中兩相(A+B)平衡時,每一個組元在 A 及 B 相中的化學勢必須相等: μ姦=μ婑 (27)
對於二元 (A及B)系中的兩相(A 和B)平衡,可用下頁圖所示的公切線圖解法求出平衡時A相的成分xa和B相的成分xB。
 合金熱力學
合金熱力學μ姦>μ婑 (28)
則i組元可自發地從A相遷移到B相。
對於如下的化學反應:
aA+bB+……→ιL+mM+…… (29)
式中A,B,……是反應物,L,M,……是反應產物;a,b,……及ι,m,……分別是A,B,……L,M,……的摩爾數,可以證明,恆溫恆壓平衡時(ΔGm=0)的關係為:
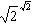 (30)
(30)
ai=γixi (31)
式中γi是活度係數,可以實驗測定。
統計熱力學 熱力學的優點是它的高度可靠性和套用的普遍性。但它不考慮物質的結構,不給出物質的具體知識,它只是一種巨觀的現象理論。統計熱力學正好彌補了熱力學的這個缺點,它從體系的具體結構,去計算熱力學函式。例如,利用下式可以計算體系的組態熵:
S=k ln W (32)
式中k是玻耳茲曼常數,W是熱力學幾率或叫狀態數。又例如:
F=-KT ln Z (33)
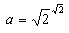 (34)
(34)
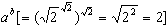 (35)
(35)
典型問題舉例 合金熱力學所研究的課題不斷在發展,現舉例介紹其思路如下:
平衡結構 主要解決合金內部幾個組元之間達到平衡時的結構形式,例如,是形成理想固溶體,或有序固溶體,還是形成金屬間化合物等等(見合金相)。
在處理平衡結構問題時,可依據具體情況,選擇(9)~(12)式的平衡判據。一般都用自由能 F來描述變化的平衡,以(11)式為平衡判據,並以自由能為最小作為變化的平衡條件。具體步驟如下:選定所要研究的成分或結構參量X(例如飽和固溶體的成分,有序固溶體的有序度,純金屬的空位飽和濃度,晶界區的平衡濃度,磁疇壁的厚度等)然後計算U和S與X的關係,代入(7)式,得到:
F=f(X,T) (36)
利用平衡系統的自由能為最小的條件:
dF/dX=f┡(X,T)=0 (37)
d2F/dX2=f"(X,T)>0 (38)
便可從(37)式求出平衡時X和T的關係。
以二元代位固溶體為例。由統計物理學公式(32),可以得出系統的摩爾混合熵(組態熵)Sm:
Sm=-R(XΑlnXΑ+XBlnXB) (39)
式中XΑ、XB分別為A和B組元的摩爾分數;R為氣體常數。
當已知固溶體的結構為完全無序排列,用統計物理方法還可計算二元固溶體內能變化:
Um=λXΑXB (40)
 (41)
(41)
Fm=λXΑXB+RT(XΑlnXΑ+XBlnXB) (42)
整個固溶體的自由能與純組元自由能FΑ、FB關係為:
Fm=XΑFΑ+XBFB+λXΑXB+RT(XΑlnXΑ+XBlnXB) (43)
令XΑ=X,則XB=1-X,並利用上式及(11)式,可得:
 (44)
(44)
 (45)
(45)
當 λ=0,即
 ,表明異類原子間的鍵能等於同類原子鍵能,合金為理想固溶體。
,表明異類原子間的鍵能等於同類原子鍵能,合金為理想固溶體。 當 λ<0,即
 ,表明異類原子間的鍵能小於同類原子間的鍵能,異類原子容易偏聚。在組元間電化學因素相差較小的情況下,合金在低溫下傾向於形成有序固溶體(或稱超點陣)。如組元間電化學因素相差較大,則合金傾向於形成金屬間化合物。 當 λ>0,即
,表明異類原子間的鍵能小於同類原子間的鍵能,異類原子容易偏聚。在組元間電化學因素相差較小的情況下,合金在低溫下傾向於形成有序固溶體(或稱超點陣)。如組元間電化學因素相差較大,則合金傾向於形成金屬間化合物。 當 λ>0,即 ,可分三種情況:①當2RT>λ>0,溶液仍為單相固溶體;②當λ=2RT,
,可分三種情況:①當2RT>λ>0,溶液仍為單相固溶體;②當λ=2RT,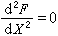 ,此時為形成兩個固溶體的臨界分層點;③當λ>2RT,
,此時為形成兩個固溶體的臨界分層點;③當λ>2RT, ,此時體系將開始形成以A或B為基的兩個固溶體,形成相區界限。
,此時體系將開始形成以A或B為基的兩個固溶體,形成相區界限。 令(44)式為零,則
 ,可以得到二元稀固溶體的飽和固溶度x與絕對溫度T的關係,即:
,可以得到二元稀固溶體的飽和固溶度x與絕對溫度T的關係,即:  (46)
(46)
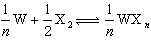 (47)
(47)
失穩條件 恆溫恆壓下,狀態失穩的必要條件是自由焓的下降,即ΔG<0【(12)式】。以液-固結晶為例,若在液相中形成半徑為r的球形晶核,並以液相為參考態,則這時的G 為:
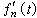 (48)
(48)
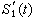 (49)
(49)
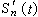 (50)
(50)
 (51)
(51)
 (52)
(52)
恆容絕熱時,狀態失穩的必要條件是內能的下降,即ΔU<0【(9)式】。以裂紋體的裂紋失穩擴展導致斷裂為例,可導出格里菲思(A.A.Griffith)斷裂理論的基本方程式(見斷裂力學)。
過程進度 套用(30)式,可以研究反應的進行程度。例如,考慮奧氏體(γ)轉變為馬氏體(M)的相變,轉變溫度(Tr)愈低,ΔG
 愈負,則形成的馬氏體量的體積分數(f)愈多。
愈負,則形成的馬氏體量的體積分數(f)愈多。 合金熱力學的能量分析方法,可以用來分析合金及其他材料的結構、性能和過程,而這三者,正是合金研究的主要問題。
參考書目
徐祖耀:《金屬材料熱力學》,科學出版社,北京,1981。
肖紀美:《合金能量學》,上海科學技術出版社,上海,1983。