二次曲線束
正文
在射影平面內,兩條二次曲線一般有四個公共點(包括實、虛或重合),通過四個公共點的二次曲線的全體叫做二次曲線束。其中四個公共點叫做基點。若已知兩條二次曲線S及
的方程分別是 
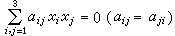及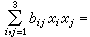
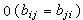，則過它們公共點的二次曲線束的方程可寫作 
，
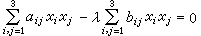交於不同的四點，則束內一切曲線都過此四點；若S，切於一點,則束內一切曲線都在這點相切，因此束內一切曲線的相交、相切情況,都和S，的相交、相切的關係一樣。根據四個基點的不同情況：四個相異點、單一切點、雙重切點、三點重合、四點重合，相應地就有五種類型的二次曲線束(見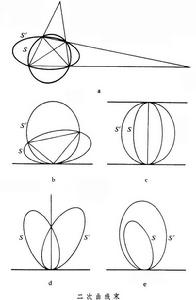
a～e)。在二次曲線束的方程中，令它的係數行列式Δ(λ)＝0，即得到一個關於λ的三次方程，由它的三個根（三個實根或一個實根二個虛根）可確定束中三條變態的二次曲線。假如四個基點是不同的實點，且其中沒有三點共線,則此四點形成一個完全四點形(見圖之a),它的三組對邊,就是束中的三條變態曲線。如已知其中兩條變態二次曲線的方程是U1U2=0和U3U4=0其中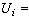
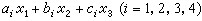，則二次曲線束的方程為
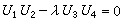。 設有一定點P(p1,p2,p3),則P關於二次曲線束S1－ λS2=0的極線方程是
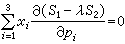,即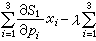
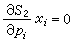。又若已知一直線l,在l上取二定點P(p1,p2，p3)和Q(q1,q2,q3)，則l關於二次曲線束的極點,應是P與Q二點的極線的交點。故有:①一個定點關於二次曲線束所有曲線的極線，形成一個直線束；②一條定直線關於二次曲線束所有曲線的極點，為一條二次曲線；可在定直線上取兩點P及Q,且令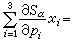
，
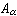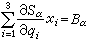(α=1,2),則P、Q兩點關於二次曲線束的極線分別為A1－λA2=0，B1-λB2=0，消去參數λ，即為二次曲線。