基本介紹
含n個未知量的線性方程組
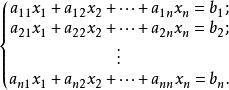 係數行列式
係數行列式 係數行列式
係數行列式由它的係數 組成的n階行列式
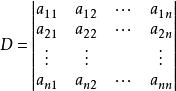 係數行列式
係數行列式叫做方程組的 係數行列式 。
係數矩陣
若線性方程組
 係數行列式
係數行列式由係數組成的矩陣
 係數行列式
係數行列式叫做方程組的 係數矩陣 。
行列式與矩陣的區別:
本質不同:行列式的結果是一個數字,而矩陣代表的是一個數字的表格。
形狀不同:行列式的行數和列數必須相等,而矩陣的行數和列數不一定相等。
克萊姆法則
若線性方程組
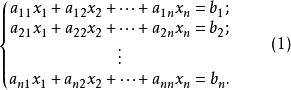 係數行列式
係數行列式的係數行列式
 係數行列式
係數行列式則方程組有唯一解,且
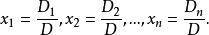 係數行列式
係數行列式這裡
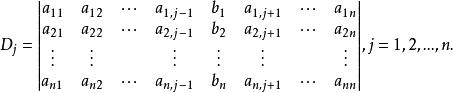 係數行列式
係數行列式由此可知,對齊次線性方程組
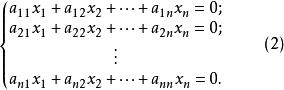 係數行列式
係數行列式若係數行列式
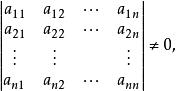 係數行列式
係數行列式則方程組只有零解。事實上,對於齊次方程組(2),有下面結論:
1. 方程組(2)只有零解的充分必要條件是係數行列式不等於零。
2. 方程組(2)有非零解的充分必要條件是係數行列式等於零。
行列式
定義
n階行列式
 係數行列式
係數行列式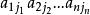 係數行列式
係數行列式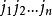 係數行列式
係數行列式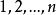 係數行列式
係數行列式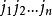 係數行列式
係數行列式 係數行列式
係數行列式為所有不同行不同列的n個元素乘積的代數和,其是的一個排列。當是偶排列時,該項符號為正;當是奇排列時,該項符號為負,即
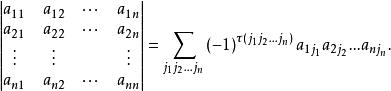 係數行列式
係數行列式行列式的性質
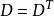 係數行列式
係數行列式性質1 行列式的行和列互換,其值不變。即行列式D與它的轉置行列式相等,。
性質2 互換行列式中任意兩行(列)的位置,行列式的正負號改變。
推論1 如果行列式中有兩行(列)的對應元素相同,則行列式等於0。
性質3用一個數k乘以行列式的某一行(列)的各元素,等於該數乘以此行列式。
推論2 行列式的某一行(列)有公因子時,可以把公因子提到行列式的外面。
推論3 若行列式的某一行(列)的元素全為0,則該行列式等於0。
推論4 如果行列式中有兩行(列)的對應元素成比例,則行列式等於0。
性質4 如果行列式的某行(列)中各元素均為兩項之和,則這個行列式可以拆成除這一行(列)以外其餘元素不變的兩個行列式的和。
性質4可推廣到某行(列)各元素為多項之和的情形。
性質5 把行列式中某一行(列)的各元素同乘以一個數k,加到另一行(列)的對應元素上,行列式的值不變。

