基本定義
平面上的直線束是指平面上通過一個固定點的所有直線的集合,也指平面上平行於一條已知直線的所有直線的集合。第一種情況中,束的所有直線所通過的點叫做束的中心,這個束本身叫做真的;第二種情況中,我們說束的中心“落在無窮遠處”,而這個束叫做假的。顯然,每一對不重合的直線包含在一個而且只有一個(真的或者假的)束里。
平行直線束
定義
平面上,一條直線以及平行於這條直線的全體直線的集合叫做平行直線束。
性質
(1)平行直線束的任何一條直線都可以完全確定這個平行直線束。
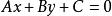 直線束
直線束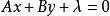 直線束
直線束 直線束
直線束(2)由已知直線 確定的平行直線束的方程為: ,其中為 參數,它可以取任意實數。
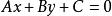 直線束
直線束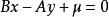 直線束
直線束 直線束
直線束(3)垂直於直線 的平行直線束的方程為: ,其中為 參數,它可以取任意實數。
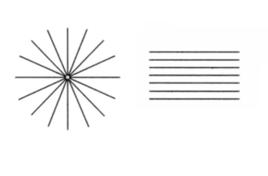
中心直線束
定義
平面上通過某個定點的直線的集合叫做一個中心直線束(簡稱線束),該定點叫做這個直線束的中心(束心)。中心直線束是平行直線束在某種意義下的特殊情形。
以已知點為中心
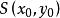 直線束
直線束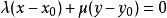 直線束
直線束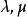 直線束
直線束以點 為中心的直線束的方程為: ,其中 均為參數,它們可以獨立地取不同時為0的任意實數。
以兩已知直線的交點為中心
中心直線束的兩條直線也確定這個直線束。要求這個直線束的方程,可先求出這兩條直線的交點,然後按照已知點為中心,求出該直線束的方程。
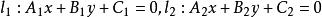 直線束
直線束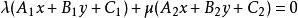 直線束
直線束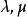 直線束
直線束設有兩條相交直線,,那么由這兩條直線所確定的中心直線束的方程為:,其中均為參數,它們可以獨立地取不同時為0的任意實數。
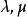 直線束
直線束直線束可用來求經過兩條相交直線交點的某直線的方程,只需用此直線的條件決定式中的比例關係。