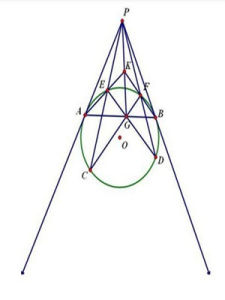
簡述
三點共線的意思:三點在同一條直線上。證明方法
方法一:取兩點確立一條直線,計算該直線的解析式.代入第三點坐標看是否滿足該解析式(直線與方程).方法二:設三點為A、B、C.利用向量證明:λAB=AC(其中λ為非零實數).
方法三:利用點差法求出AB斜率和AC斜率,相等即三點共線.
方法四:用梅涅勞斯定理.
方法五:利用幾何中的公理“如果兩個不重合的平面有一個公共點,那么它們有且只有一條過該點的公共直線”.可知:如果三點同屬於兩個相交的平面則三點共線.
方法六:運用公(定)理“過直線外一點有且只有一條直線與已知直線平行(垂直)”.其實就是同一法.
方法七:證明其夾角為180°.
方法八:設ABC,證明△ABC面積為0.
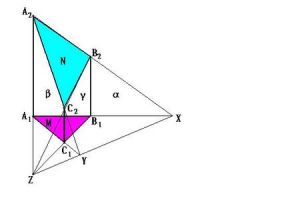 三點共線
三點共線方法九:帕普斯定理.
方法十:利用坐標證明。即證明x1y2=x2y1.
方法十一:位似圖形性質.