定義
 p級數
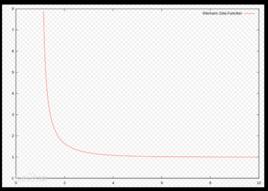
p級數定義. 對任意的正實數,稱下列級數
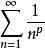 p級數
p級數 p級數
p級數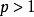 p級數
p級數 p級數
p級數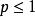 p級數
p級數 p級數
p級數 p級數
p級數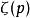 p級數
p級數 p級數
p級數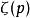 p級數
p級數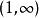 p級數
p級數為級數。顯然,當時,級數收斂,當,級數發散。當級數收斂時,記為級數收斂值。易知是上的光滑函式 。
特殊值
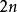 p級數
p級數1)對任意的正偶數,有
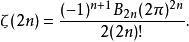 p級數
p級數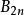 p級數
p級數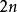 p級數
p級數其中,是第個伯努利數。對任意的正奇數,目前還沒有這樣的簡單表達式。
2)
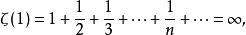 p級數
p級數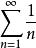 p級數
p級數也稱為調和級數,應此,由上式可知調和級數是發散的。
3)
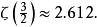 p級數
p級數4)
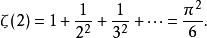 p級數
p級數5)
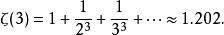 p級數
p級數6)
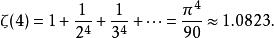 p級數
p級數歐拉乘積公式
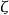 p級數
p級數函式與素數之間有一重要的關係,即歐拉乘積公式,最早由數學家歐拉發現 。即為
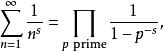 p級數
p級數其中,表達式右邊為
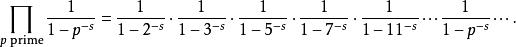 p級數
p級數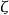 p級數
p級數歐拉乘積公式表明函式和素數之間有千絲萬縷的聯繫。
由歐拉乘積公式,我們有
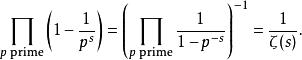 p級數
p級數 p級數
p級數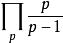 p級數
p級數當時,歐拉乘積公式左邊為調和級數,是發散的,歐拉乘積公式右邊為,這表明素數是無窮多個。除此之外,上述公式還有很多其它用處。如歐拉乘積公式可用於計算隨機選取的整數互質的漸近機率。
黎曼函式
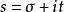 p級數
p級數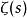 p級數
p級數定義. 在複平面上,對任意,定義黎曼函式為
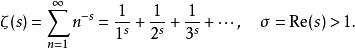 p級數
p級數或者由下述積分給出
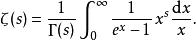 p級數
p級數其中
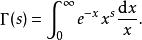 p級數
p級數黎曼函式和黎曼猜想有關。而目前黎曼猜想是數學上還未解決的一個重要的猜想,其猜想是非平凡的零點的分布都位於複平面上 Re(s)=1/2 的直線上。進一步的了解參見黎曼猜想。