證明方法
作差法
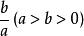 糖水不等式
糖水不等式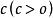 糖水不等式
糖水不等式真分數 ,在分子分母同時加上一個 ,即:
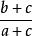 糖水不等式
糖水不等式則用作差法表示為:
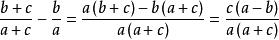 糖水不等式
糖水不等式∵a>b>0,c>0
∴
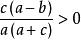 糖水不等式
糖水不等式∴一個真分數在分母分子同時加上一個正數時,分數將變大。
糖水不等式:
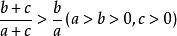 糖水不等式
糖水不等式成立。
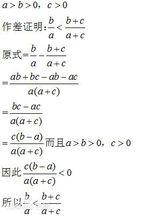 糖水不等式
糖水不等式作商法
根據作商法可知:
若糖水不等式成立,則不等式:
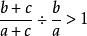 糖水不等式
糖水不等式也成立。
由不等式左邊得:
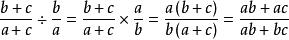 糖水不等式
糖水不等式即:
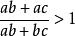 糖水不等式
糖水不等式∵a>b>0且c>0
∴ab>0,ac>bc>0
即:
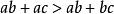 糖水不等式
糖水不等式∴不等式:
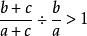 糖水不等式
糖水不等式成立,糖水不等式:
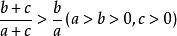 糖水不等式
糖水不等式也成立。
分析法
欲使糖水不等式成立,即:
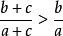 糖水不等式
糖水不等式只需:
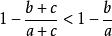 糖水不等式
糖水不等式只需:
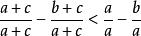 糖水不等式
糖水不等式只需:
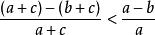 糖水不等式
糖水不等式只需:
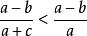 糖水不等式
糖水不等式只需:
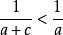 糖水不等式
糖水不等式只需:
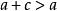 糖水不等式
糖水不等式又∵c>0
∴此不等式顯然成立,糖水不等式:
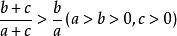 糖水不等式
糖水不等式也成立。
其他方法
1.綜合法
2.構造函式法
3.定比分點公式法
生活啟示
在以後學習中,不僅掌握知識本身,還要多體會知識產生、發展背景、及其套用,以達到舉一反三、融會貫通的目的;從而得出思考與反思的必要環節。
實際套用
在溶液中,判斷溶質的質量分數的大小時,經常用到該不等式。
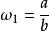 糖水不等式
糖水不等式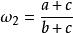 糖水不等式
糖水不等式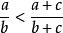 糖水不等式
糖水不等式現有質量為b的物質A的水溶液,其中含有質量為a的物質A,則此時該溶液的溶質的質量分數
。向該溶液中再加入質量為c的物質A,並充分攪拌,物質A全部溶解,則此時溶液的溶質的質量分數。根據“糖水不等式”,有,
即可得到
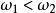 糖水不等式
糖水不等式則加入物質A後的溶液中,溶質的質量分數大於加入物質A之前的溶液中溶質的質量分數,即加入物質A前濃度小於加入物質A後的濃度。

