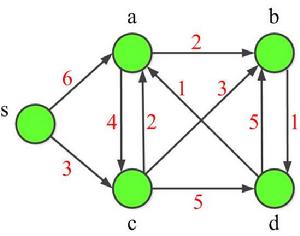
使用條件
Floyd-Warshall 算法用來找出每對點之間的最短距離。它需要用鄰接矩陣來儲存邊,這個算法通過考慮最佳子路徑來得到最佳路徑。
算法介紹
單獨一條邊的路徑也不一定是最佳路徑。 從任意一條單邊路徑開始。所有兩點之間的距離是邊的權的和,(如果兩點之間沒有邊相連, 則為無窮大)。 從第一個頂點開始,依次將每個頂點作為媒介 k,然後對於每一對頂點 u 和 v ,查看其是否存在一條經過 k 的,距離比已知路徑更短的路徑,如果存在則更新它。
即dist[k](i,j) = min(dist[k-1](i,j),dist[k-1](i,k)+dist[k-1](k,j)。// dist[k](i,j) 為媒介結點為k時從節點i到節點j的最短距離
For i←1to n do
For j←1to n do
dist(i,j) = weight(i,j)
For k←1to n do// k為“媒介節點” {一定要先枚舉媒介節點}
For i←1to n do
For j←1to n do
if(dist(i,k) + dist(k,j) < dist(i,j))then// 是否是更短的路徑?
dist(i,j) = dist(i,k) + dist(k,j)
這個算法的效率是O( V^3)。它需要鄰接矩陣來儲存圖。
這個算法很容易實現,只要幾行。
即使問題是求單源最短路徑,還是推薦使用這個算法,如果時間和空間允許(只要有放的下鄰接矩陣的空間,時間上就沒問題)。
計算每一對頂點間的最短路徑(floyd算法)
例題
設計公共汽車線路(1)
現有一張城市地圖,圖中的頂點為城市,有向邊代表兩個城市間的連通關係,邊上的權即為距離。現在的問題是,為每一對可達的城市間設計一條公共汽車線路,要求線路的長度在所有可能的方案里是最短的。
輸入:
市數,1≤n≤20)
e (有向邊數1≤e≤210)
以下e行,每行為邊(i,j)和該邊的距離wij(1≤i,j≤n)
輸出:
k行,每行為一條公共汽車線路
分析:本題給出了一個帶權有向圖,要求計算每一對頂點間的最短路徑。這個問題雖然不是圖的連通性問題,但是也可以借鑑計算傳遞閉包的思想:在枚舉途徑某中間頂點k的任兩個頂點對i和j時,將頂點i和頂點j中間加入頂點k後是否連通的判斷,改為頂點i途徑頂點k至頂點j的路徑是否為頂點i至頂點j的最短路徑(1≤i,j,k≤n)。 顯然三重循環即可計算出任一對頂點間的最短路徑。設 n—有向圖的結點個數;path—最短路徑集合。其中path[i,j]為vi至vj的最短路上vj的前趨結點序號(1≤i,j≤n);adj—最短路徑矩陣。初始時為有向圖的相鄰矩陣
我們用類似傳遞閉包的計算方法反覆對adj矩陣進行運算,最後使得adj成為存儲每一對頂點間的最短路徑的矩陣
Var adj:array[1‥n,1‥n] of real;
path:array[1‥n,1‥n] of 0‥n;
計算每一對頂點間最短路徑的方法如下:
首先枚舉路徑上的每一個中間頂點k(1≤k≤n);然後枚舉每一個頂點對(頂點i和頂點j,1≤i,j≤n)。如果i頂點和j頂點間有一條途徑頂點k的路徑,且該路徑長度在目前i頂點和j頂點間的所有條途徑中最短,則該方案記入adj[i,j]和path[i,j]
adj矩陣的每一個元素初始化為∞;
for i←1 to n do {初始時adj為有向圖的相鄰矩陣,path存儲邊信息}
for j←1 to n do
if wij<>0 then begin adj[i,j]←wij;path[i,j]←j;end{then}
else path[i,j]←0;
for k←1 to n do {枚舉每一個中間頂點}
for i←1 to n do {枚舉每一個頂點對}
for j←1 to n do
if adj[i,k]+adj[k,j]<adj[i,j] {若vi經由vk 至vj的路徑目前最優,則記下}
then begin
adj[i,j]←adj[i,k]+adj[k,j];
path[i,j]←path[i,k];
end,{then}
計算每一對頂點間最短路徑時間複雜度為W(n3)。算法結束時,由矩陣path可推知任一結點對i、j之間的最短路徑方案是什麼
Procedure print(i,j);
begin
if i=j then 輸出i
else if if path[i,j]=0
then 輸出結點i與結點j之間不存在通路
else begin
print (i,path[i,j]); {遞歸i頂點至j頂點的前趨頂點間的最短路徑}
輸出j;
end;{else}
end;{print}
由此得出主程式
距離矩陣w初始化為0;
輸入城市地圖信息(頂點數、邊數和距離矩陣w);
計算每一對頂點間最短路徑的矩陣path;
for i←1 to n do {枚舉每一個頂點對}
for j←1 to n do if path[i,j]<>0 {若頂點i可達頂點j,則輸出最短路徑方案}
then begin print(i,j);writeln;end;{then}
P ASCAL語言
program floyd;
var st,en,f:integer;
k,n,i,j,x:integer;
a:array[1..10,1..10] of integer;
path:array[1..10,1..10] of integer;
begin
readln(n);
for i:=1 to n do
begin
for j:=1 to n do
begin
read(k);
if k<>0 then
a[i,j]:=k
else
a[i,j]:=maxint;
path[i,j]:=j;
end;
readln;
end;
for x:=1 to n do
for i:=1 to n do
for j:=1 to n do
if a[i,j]>a[i,x]+a[x,j] then
begin
a[i,j]:=a[i,x]+a[x,j];
path[i,j]:=path[i,x];
end;
readln(st,en);
writeln(a[st,en]);
f:=st;
while f<> en do
begin
write(f);
write('-->');
f:=path[f,en];
end;
writeln(en);
end.