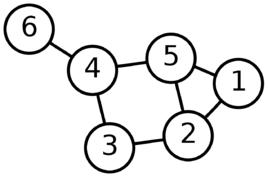
問題介紹
最短路徑問題是圖論研究中的一個經典算法問題，旨在尋找圖（由結點和路徑組成的）中兩結點之間的最短路徑。算法具體的形式包括：
•確定起點的最短路徑問題-即已知起始結點，求最短路徑的問題。適合使用Dijkstra算法。
•確定終點的最短路徑問題-與確定起點的問題相反，該問題是已知終結結點，求最短路徑的問題。在無向圖中該問題與確定起點的問題完全等同，在有向圖中該問題等同於把所有路徑方向反轉的確定起點的問題。
•確定起點終點的最短路徑問題-即已知起點和終點，求兩結點之間的最短路徑。
•全局最短路徑問題-求圖中所有的最短路徑。適合使用Floyd-Warshall算法。
用於解決最短路徑問題的算法被稱做“最短路徑算法”，有時被簡稱作“路徑算法”。最常用的路徑算法有：
•Dijkstra算法
•A*算法
•Bellman-Ford算法
•SPFA算法（Bellman-Ford算法的改進版本）
•Floyd-Warshall算法
•Johnson算法
•Bi-DirectionBFS算法
Dijkstra算法
簡介
戴克斯特拉算法（英語：Dijkstra'salgorithm）是由荷蘭計算機科學家艾茲赫爾·戴克斯特拉提出。迪科斯特拉算法使用了廣度優先搜尋解決賦權有向圖的單源最短路徑問題，算法最終得到一個最短路徑樹。該算法常用於路由算法或者作為其他圖算法的一個子模組。舉例來說，如果圖中的頂點表示城市，而邊上的權重表示城市間開車行經的距離，該算法可以用來找到兩個城市之間的最短路徑。
該算法的輸入包含了一個有權重的有向圖G，以及G中的一個來源頂點S。我們以V表示G中所有頂點的集合。每一個圖中的邊，都是兩個頂點所形成的有序元素對。(u,v)表示從頂點u到v有路徑相連。我們以E表示G中所有邊的集合，而邊的權重則由權重函式w:E→[0,∞]定義。因此，w(u,v)就是從頂點u到頂點v的非負權重（weight）。邊的權重可以想像成兩個頂點之間的距離。任兩點間路徑的權重，就是該路徑上所有邊的權重總和。已知有V中有頂點s及t，Dijkstra算法可以找到s到t的最低權重路徑(例如，最短路徑)。這個算法也可以在一個圖中，找到從一個頂點s到任何其他頂點的最短路徑。
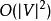最短路線問題
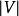最短路線問題
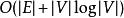最短路線問題
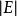最短路線問題最初的戴克斯特拉算法不採用最小優先權佇列，時間複雜度是 (其中 為圖的頂點個數)。通過斐波那契堆實現的迪科斯徹算法時間複雜度是 (其中 是邊數)（Fredman&Tarjan1984）。對於不含負權的有向圖，這是已知的最快的單源最短路徑算法。
算法描述
這個算法是通過為每個頂點v保留所找到的從s到v的最短路徑來工作的。初始時，原點s的路徑權重被賦為0（d[s]=0）。若對於頂點s存在能直接到達的邊（s,m），則把d[m]設為w（s,m）,同時把所有其他（s不能直接到達的）頂點的路徑長度設為無窮大，即表示我們不知道任何通向這些頂點的路徑（對於所有頂點的集合V中的任意頂點v，若v不為s和上述m之一，d[v]=∞）。當算法結束時，d[v]中存儲的便是從s到v的最短路徑，或者如果路徑不存在的話是無窮大。
邊的拓展是Dijkstra算法的基礎操作：如果存在一條從u到v的邊，那么從s到v的最短路徑可以通過將邊（u,v）添加到尾部來拓展一條從s到v的路徑。這條路徑的長度是d[u]+w(u,v)。如果這個值比已知的d[v]的值要小，我們可以用新值來替代當前d[v]中的值。拓展邊的操作一直運行到所有的d[v]都代表從s到v的最短路徑的長度值。此算法的組織令d[u]達到其最終值時，每條邊（u,v）都只被拓展一次。
算法維護兩個頂點集合S和Q。集合S保留所有已知最小d[v]值的頂點v，而集合Q則保留其他所有頂點。集合S初始狀態為空，而後每一步都有一個頂點從Q移動到S。這個被選擇的頂點是Q中擁有最小的d[u]值的頂點。當一個頂點u從Q中轉移到了S中，算法對u的每條外接邊(u,v)進行拓展。
A*搜尋算法
A*搜尋算法，俗稱 A星算法。這是一種在圖形平面上，有多個節點的路徑，求出最低通過成本的算法。常用於遊戲中的NPC的移動計算，或網路遊戲的BOT的移動計算上。
該算法綜合了Best-First Search和Dijkstra算法的優點：在進行啟發式搜尋提高算法效率的同時，可以保證找到一條最優路徑（基於評估函式）。
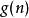最短路線問題
最短路線問題
最短路線問題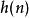 最短路線問題在此算法中，如果以 表示從起點到任意頂點 的實際距離， 表示任意頂點到目標頂點的估算距離（根據所採用的評估函式的不同而變化），那么A*算法的估算函式為：
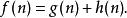最短路線問題這個公式遵循以下特性：
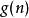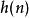最短路線問題 最短路線問題 最短路線問題 最短路線問題如果為0，即只計算任意頂點到目標的評估函式，而不計算起點到頂點的距離，則算法轉化為使用貪心策略的Best-First Search，速度最快，但可能得不出最優解；
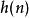最短路線問題 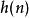最短路線問題如果不高於實際到目標頂點的距離，則一定可以求出最優解，而且越小，需要計算的節點越多，算法效率越低，常見的評估函式有——歐幾里得距離、曼哈頓距離、切比雪夫距離；
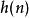最短路線問題 最短路線問題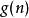 最短路線問題 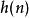最短路線問題如果為0，即只需求出起點到任意頂點的最短路徑，而不計算任何評估函式，則轉化為單源最短路徑問題，即Dijkstra算法，此時需要計算最多的定點。
福特算法
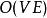最短路線問題貝爾曼-福特算法（英語：Bellman–Ford algorithm），求解單源最短路徑問題的一種算法，由理察·貝爾曼（Richard Bellman） 和萊斯特·福特創立的。它的原理是對圖進行V-1次鬆弛操作，得到所有可能的最短路徑。其優於迪科斯徹算法的方面是邊的權值可以為負數、實現簡單，缺點是時間複雜度過高，高達。但算法可以進行若干種最佳化，提高了效率。
弗洛伊德算法
Floyd-Warshall算法（英語：Floyd-Warshall algorithm），中文亦稱 弗洛伊德算法，是解決任意兩點間的最短路徑的一種算法，可以正確處理有向圖或負權（但不可存在負權迴路）的最短路徑問題，同時也被用於計算有向圖的傳遞閉包。
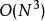最短路線問題
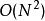最短路線問題Floyd-Warshall算法的時間複雜度為，空間複雜度為。
