定義
Floyd-Warshall 算法用來找出每對點之間的最短距離。它需要用鄰接矩陣來儲存邊,這個算法通過考慮最佳子路徑來得到最佳路徑。 注意單獨一條邊的路徑也不一定是最佳路徑。
思想
從任意一條單邊路徑開始。所有兩點之間的距離是邊的權,或者無窮大,如果兩點之間沒有邊相連。
對於每一對頂點 u 和 v,看看是否存在一個頂點 w 使得從 u 到 w 再到 v 比己知的路徑更短。如果是更新它。
實現
Pascal程式:
for i:= 1 to n do
for j:= 1 to n do
read(f[i,j]);
for k:= 1 to n do
for i:= 1 to n do
for j:= 1 to n do
if (i<>j)and(i<>k)and(j<>k)and(f[i,k]+f[k,j]<f[i,j]) then
f[i,j]:=f[i,k]+f[k,j];
總評
時間複雜度O(n^3),只要有存下鄰接矩陣的空間,時間一般沒問題,並且不必擔心負權邊的問題。
圖文
弗洛耶德算法(Floyed算法):
基本思想:求解所有點間的路徑需要進行n次試探。對於頂點i到頂點j的路徑長度,首先考慮讓路徑經過頂點1,比較路徑(i,j)和(i,1,j)的長度取其短者為當前求得的最短路徑長度。對每一對頂點的路徑都做這樣的試探,則可求得一個矩陣設為A(1),求n次即得每對頂點間的最短路徑A(n)。A(0)=A:鄰接矩陣。如下圖:
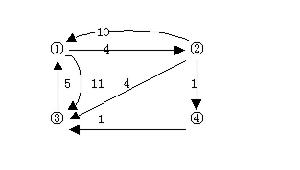

程式如下:
program floyed;
const n=4;
var
cost,a:array[1..n,1..n]of integer;
p:array[1..n,1..n] of 0..n;
i,j,k:integer;
procedure init;
var i,j:integer;
begin
for i:=1 to n do
for j:=1 to n do
begin
read(cost[i,j]);
a[i,j]:=cost[i,j];
p[i,j]:=0;
end;
end;
procedure path(i,j:integer);
var k:integer;
begin
k:=p[i,j];
if k<>0 then begin path(i,k);write('->',k);path(k,j);end
end;
begin
init;
for k:=1 to n do
for i:=1 to n do
for j:=1 to n do
if a[i,k]+a[k,j]<a[i,j] then
begin
a[i,j]:=a[i,k]+a[k,j];
p[i,j]:=k;
end;
for i:=1 to n do
for j:=1 to n do
if i<>j then
begin
writeln('a[',i,',',j,']=",a[i,j]);
write(i);
path(i,j);
writeln("->',j)
end;
end.
注意:弗洛耶德算法(Floyed算法)思想可用與判斷有向圖中任意兩點是否連通?算法如下:
for k:=1 to n do
for i:=1 to n do
for j:=1 to n do
if (a[i,k]=1)and (a[k,j]=1) then a[i,j]=1 (a[i,j]=1表示i可達j,a[i,j]=0表示i不可達j)。
