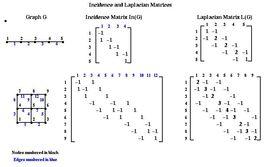
定義
如果f是二階可微的實函式，則f的拉普拉斯運算元定義為：
(1) f的拉普拉斯運算元也是笛卡兒坐標系中的所有非混合二階偏導數求和：
(2) 作為一個二階微分運算元，拉普拉斯運算元把C函式映射到C函式，對於k ≥ 2。表達式(1)（或(2)）定義了一個運算元Δ : C(R) → C(R)，或更一般地，定義了一個運算元Δ : C(Ω) → C(Ω)，對於任何開集Ω。
對於階躍狀邊緣，導數在邊緣點出現零交叉，即邊緣點兩旁二階導數取異號。據此，對數字圖像{f（i，j）}的每個像素，取它關於x軸方向和y軸方向的二階差分之和，表示為
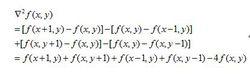Laplacian運算元運算模板
函式的拉普拉斯運算元也是該函式的黑塞矩陣的跡,可以證明，它具有各向同性，即與坐標軸方向無關，坐標軸旋轉後梯度結果不變。如果鄰域系統是4 鄰域，Laplacian 運算元的模板為：
| 0 | 1 | 0 |
| 1 | -4 | 1 |
| 0 | 1 | 0 |
如果鄰域系統是8 鄰域，Laplacian 運算元的模板為：
| 1 | 1 | 1 |
| 1 | -8 | 1 |
| 1 | 1 | 1 |
前面提過，Laplacian 運算元對噪聲比較敏感，所以圖像一般先經過平滑處理，因為平滑處理也是用模板進行的，所以，通常的分割算法都是把Laplacian 運算元和平滑運算元結合起來生成一個新的模板。
結果對比
Laplacian運算元
Laplacian運算元