計算空氣動力學
正文
這一空氣動力學的學科分支自60年代後期以來得到了迅速的發展，主要原因是：利用計算空氣動力學的方法，不但可以對外形給定的飛行器進行空氣動力學的分析，還可以按預定的氣動特性要求設計飛行器的外形，得出流場中物理量的細節分布，不存在風洞實驗中洞壁和支架干擾等一系列麻煩問題；另一個原因是計算機的運算能力迅速提高，計算費用下降。計算空氣動力學在飛行器的空氣動力學分析和設計中發揮著越來越大的作用，使設計過程發生了根本性的變革。
計算空氣動力學數學模型 在實驗觀察的基礎上，對流場的物理本質進行深入的理解和分析，建立起描述流場的合理的數學模型，為計算空氣動力學提供出發的基本方程組和初、邊值條件。在航空、航天方面，飛行器周圍的流場非常複雜,且隨飛行器的飛行高度和飛行速度有很大變化,必須考慮空氣的連續或非連續性、壓縮性、熱傳導性、粘性和其他物理、化學過程，因此基本方程組是十分複雜的。例如，對於不能視為連續介質的稀薄空氣，描述其運動的基本方程組為玻爾茨曼方程，這是一非線性的偏微分-積分方程，對於可視為連續介質的空氣,描述其運動的基本方程組為納維爾-斯托克斯方程(簡稱N-S方程)，這是一非線性的偏微分方程組。N-S 方程可由玻爾茨曼方程導出,雖然比玻爾茨曼方程簡單了許多,但是仍嫌複雜。現代即使用最有效的數值計算方法和容量最大、速度最快的計算機，也還遠遠不能通過求解這一方程組來模擬真實飛行器的繞流。因此，為了解決實際工程問題,必須根據實際問題的物理特徵對 N-S方程進行不同程度的簡化，建立各種近似的數學模型和數學方程。廣泛採用的簡化近似方程有：線性位流方程、非線性位流方程、非線性歐拉方程、粘性邊界層方程、粘性薄層近似方程、拋物化N-S方程和完全N-S方程等。
①線性位流方程：假設氣體無粘性，存在速度位對繞細長機身薄翼及其組合體的純亞音速和純超音速小迎角繞流,可以進一步假設這類物體對流場產生小擾動,因而可以將速度位方程線性化，從而給出線性位流方程。
②非線性位流方程：假設氣體無粘性，對含有弱激波的跨音速繞流問題，即使在小擾動假定下，也不能將方程線性化，但仍可假設存在速度位，這時採用的方程為非線性位流方程。
③非線性歐拉方程：由L.歐拉建立的只假設氣體無粘性的方程。它比上面兩種方程更為精確。對於具有較強激波或有分離渦面的流動和其他一些複雜的問題，在求氣動力時常採用這種方程。
④邊界層方程：雷諾數(Re)很高的氣流繞過飛行器表面時，在物面很薄的流體層內，粘性力的作用不可忽略，以
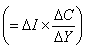為小參數簡化N-S 方程而得到的一級近似方程稱為邊界層方程，它是德國流體力學家L.普朗特提出的，又稱普朗特邊界層方程。 ⑤粘性薄層方程：仍假設粘性的影響主要集中在飛行器表面附近的薄層內。但以ε為小參數簡化N-S方程時，準確度比邊界層方程更高一階，這樣獲得的方程稱為粘性薄層近似方程。與邊界層方程比較，它適用的雷諾數範圍更大，且考慮了粘性、無粘性的相互干擾作用。
⑥拋物化的N-S方程：在N-S方程中略去一切沿主流方向的二階粘性耗散項後所得到的方程。這樣獲得的方程組在數學性質上是拋物型的,所以稱拋物化的N-S方程。為了便於區別,一般把不經過任何簡化的N-S方程稱為完全的N-S方程。
數值計算方法 為了求解上面幾類數學模型的方程組，必須採用有效的數值方法。數值計算方法的有效性常常與方程的數學性質有關。例如對於線性位流方程，採用有限基本解法或面板法是很有效的。對於橢圓型方程，有限元素法也是有效的。在求解各類非線性氣動方程時，廣泛採用有限差分法和有限體積法。此外有限元素法和譜分析法也在發展中。
計算機技術 利用計算機可以完成數值計算、公式推導、格線生成、計算結果分析和計算流場的圖像顯示。為了完成複雜的三維流場計算,需要發展巨型計算機,並採用並行處理、流水線處理或多方處理的並行操作。中國在80年代初已研製成功億次“銀河”大型計算機。為了滿足公式推導和流場顯示等要求，還鬚髮展有關計算機軟體。計算機計算能力的提高，不會削弱氣動理論研究的發展，相反，它能加深人們對複雜流動現象的認識和理解。計算空氣動力學的發展並不排斥風洞實驗研究工作。兩者結合，互相補充，逐步實現一體化，是飛行器設計和氣動研究的發展方向。
