HL定理

HL定理是證明兩個直角三角形全等的定理，通過證明兩個直角三角形直角邊和斜邊對應相等來證明兩個三角形全等。判定定理為：如果兩個直角三角形的斜邊和一條直角邊對應相等，那么這兩個直角三角形全等（簡記為HL)是一種特殊判定方法，可轉換為ASA

基本信息

• 中文名：HL定理
• 英文名：HL theorem

• 中文名稱：HL定理
• 英文名：HL theorem
• 三角形全等：簡稱HL(或斜邊直角邊
• 幾何語言：Rt △ABC ≌ Rt△A'B'C'(HL).
• 勾股定理：a²+b²=c²

定理內容

斜邊和 一條直角邊對應相等的兩個直角三角形全等。（可以簡寫成“HL”）

定理條件

HL定理

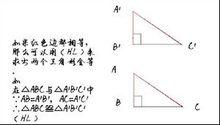HL定理

證明兩Rt△全等的條件：兩個直角（Rt）三角形的一條斜邊與一條直角邊分別對應相等，則兩個直角（Rt）三角形全等，簡稱HL 「記住：前提是一定要是直角三角形（Rt)」

H是hypotenuse(斜邊)的縮寫，L是leg(直角邊)的縮寫

定理證明

已知：Rt△ABC和Rt△DEF中，∠B=∠E=90°，AC=DF，AB=DE.

求證：△ABC≌△DEF.

HL定理

證明：在Rt△ABC中，BC=.

HL定理

在Rt△DEF中，EF=,

∵AC=DF，AB=DE.

∴BC=EF

∵AC=DF,BC=EF,AB=DE.

∴△ABC≌△DEF（SSS）.