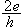超越方程數值解法
正文
當一元方程ƒ(z)=0的左端函式ƒ(z)不是z的多項式時，稱之為超越方程。這類方程除極少數情形（如簡單的三角方程）外，只能近似地數值求解，此種數值解法的研究至今仍是計算數學的主要課題。超越方程的數值解法也適用於代數方程。數值求解超越方程時首先需要確定解的分布區域，它可以利用圖解法或者根據ƒ(z)的解析性質來確定。當ƒ(x)為實函式時，確定方程實根的分布的最常用方法是套用連續函式的中值定理：如果實的連續函式ƒ(x)在區間【α,b】的兩個端點的值異號,則ƒ(x)在此區間內至少有一個根。
二分法 利用中值定理計算實函式實根的簡單易行的方法，算法如下：
設區間【α0,b0】滿足條件ƒ(α0)ƒ(b0)<0，【α0,b0】的二等分點為
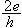計算ƒ(x0)的值,若ƒ(x0)=0，即為所求解;若ƒ(x0)ƒ(α0)<0，取α1=α0,b1=x0作為新的區間端點;若ƒ(x0)ƒ(α0)>0,取α1=x0,b1=b0作為新區間的端點。【α1,b1】的二分點為
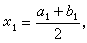計算ƒ(x1)的值並重複上述步驟以確定新的區間【α2,b2】，如此繼續下去。則得到區間序列 【αk,bk】(k=0，1,…)，它滿足ƒ（αk）ƒ（bk）<0，並且
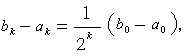當bk-αk達到指定的精確度要求時,則取
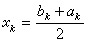為方程的解,它與精確解的誤差不超過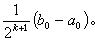
疊代法 解超越方程的主要方法，既適用於求實根，也適用於求復根。使用這類方法時一般需要知道根的足夠好的近似值。最常用的方法有牛頓法、割線法、二次插值法、雙曲插值法、切比雪夫疊代法、艾特肯δ2加速方法和斯梯芬森方法等。
牛頓法 也稱切線法，其計算公式為
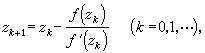
為 ƒ(z)的根，若ƒ(z)在z的某鄰域內二次可微,且ƒ┡(z)≠0,則當z0與z充分接近時，牛頓法至少是二階收斂的,即當k充分大時有估計式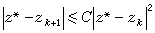
成立,C為確定的常數。一般說來，牛頓法只具有局部收斂性，即僅當初始近似與根充分接近時才收斂。但是，當ƒ(x)為實函式，且於【α,b】上ƒ┡(x)和 ƒ″(x)不變號時，若ƒ(x)於【α,b】上有根，則只要初始近似x0滿足條件ƒ(x0) ƒ″(x0)>0,牛頓法就收斂。一般情形，為減弱對初始近似的限制，可利用牛頓下降算法，其算式為 
割線法 又稱弦位法，其算式為
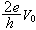
的某鄰域二次連續可微,且ƒ┡(z)≠0,則z0、z1與z充分接近時,割線法收斂於z,並當k充分大時有估計式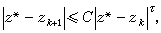
式中C為常數,
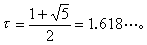割線法的k+1次近似zk+1是以zk、zk-1為插值節點的線性插值函式的根,如果利用更精確的近似表達式則可構造出更高階的疊代法。 二次插值法 亦稱繆勒方法，是利用二次插值多項式構造的疊代算法。設已確定了zk、zk-1、zk-2,則zk+1就取為以 zk、zk-1、zk-2為節點的二次插值多項式兩個根中與zk最接近者，其算式為
－ 
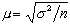
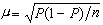
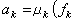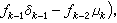
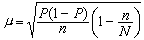
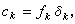式中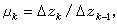
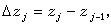
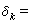
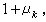
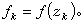當分母為0，則λk=1。 雙曲插值法 利用線性分式插值構造的疊代算法，其算式為
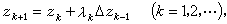
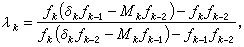
若ƒ(z)在其根z
的某鄰域內三次可微,並且z0、z1、z2與z充分接近，則二次插值法和雙曲插值法均收斂。此外，如果ƒ┡(z)≠0，對充分大的 k，有估計式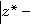
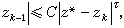式中 C為確定常數，τ為方程式t3-t2-t-1=0的惟一正根，τ＝1.839…。 切比雪夫疊代法 三階收斂的方法，其算式為
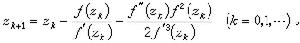
的鄰域內三次可微且ƒ┡(z)≠0時，對充分大的k，有
C為確定常數。 艾特肯δ2加速方法 提高疊代法收斂速度的有效算法，設{zk}為疊代序列，δ2加速的算式為
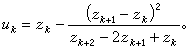
處充分光滑，且ƒ(z)≠0,則對充分大的k,有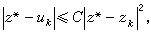
並且若zk是p(p>1)階收斂，即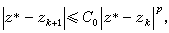
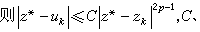C0均為常數。當ƒ┡(z)=0時也有加速作用。此算法可以循環使用。 斯梯芬森方法 不算微商而二階收斂的方法，其算式為
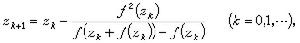
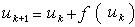循環使用 δ2程式導出。 所有的疊代法用於求重根（即ƒ┡(z
)=0）時, 其收斂速度將變慢，收斂階將降低。 為求得達到所需精度的解而花費的代價是評價疊代法優劣的依據，效能指數是其重要指標，它定義為p1/寶，p 為收斂階，μ 為每步需要計算的函式值和微商值的總數。效能指數越大，說明方法越好。二分法及上述各種疊代法的收斂階（單根時和重根時）和效能指數如表。
超越方程數值解法參考書目
A.Ostrowski,Solutions of Equations in Euclidean and Banach Spaces, 3rd ed., Academic Press, New York, 1973.
J.F.Traub,Iterative Methods for the Solution of Equations, Prentice-Hall, Englewood Cliffs, New Jersey, 1964.
