一元五次方程

只含有一個未知數（即“元”），並且未知數的最高次數為5（即“次”）的整式方程叫做一元五次方程（英文名：Quintic Equation）。一元五次方程的標準形式（即所有一元五次方程經整理都能得到的形式）是ax+bx+cx+dx+ex+f=0（a,b,c,d,e,f為常數，x為未知數，且a≠0）。

基本信息

• 中文名：一元五次方程
• 其他外文名：Quintic Equation

• 方程：ax^5+bx^4+cx^3+dx^2+ex+f=0
• 條件：a,b,c,d,e,f∈R，且a≠0
• 係數：a，b，c，d，e
• 常數：f
• 現有公式：天珩公式
• 類型：整式方程
• 領域：數學

方程的定義

在一個等式中，只含有一個未知數，且未知數的最高次數是5次的整式方程叫做一元五次方程。

方程標準型

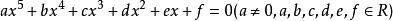一元五次方程

形如 的方程是一元五次方程的標準型。

解法

天珩公式

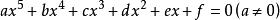一元五次方程

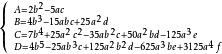一元五次方程

本公式判別法的缺點是僅可求解實係數的部分五次方程。重根判別式：

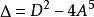一元五次方程

總判別式

(1)若A=B=C=D=0，則方程有一個五重實根。

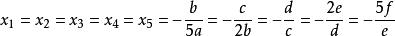一元五次方程

(2)若AD≠0，B=C=Δ=0，則方程有五個實根，其中有兩對二重根。

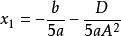一元五次方程

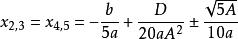一元五次方程

,

(3)若B=C=0，Δ>0，則方程有一個實根和兩對不等共軛虛根。

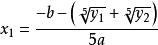一元五次方程

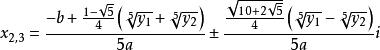一元五次方程

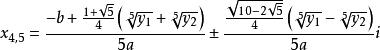一元五次方程

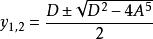一元五次方程

其中，

(4)若B=C=0，Δ<0，則方程有五個不等實根。

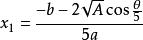一元五次方程

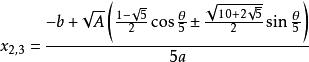一元五次方程

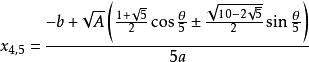一元五次方程

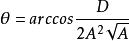一元五次方程

其中，

複數域內通用公式

先將方程配方：方程兩邊同時除以a，後令y=x+b/5a，即x=y-b/5a，化為關於y的一元五次方程：

y +py +qy +ry+s=0

若滿足q=p -5r=0，則方程可用以下方法求解：

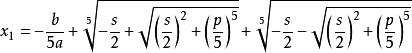一元五次方程

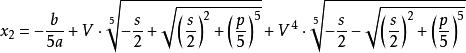一元五次方程

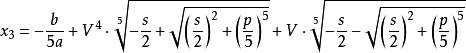一元五次方程

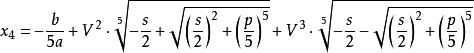一元五次方程

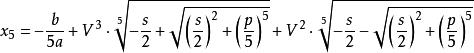一元五次方程

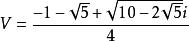一元五次方程

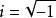一元五次方程

其中，V是1的一個五次方根且不為1。可取，

遇虛數開方時，可使用如下公式：

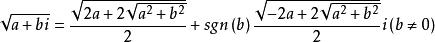一元五次方程

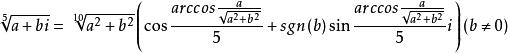一元五次方程